网站建设构建方案长治网站seo
规划论及MATLAB计算
1、线性规划
问题的提出
例1. 某工厂在计划期内要安排甲、乙两种产品的生产,已知生产单位产品所需的资源A、B、C的消耗以及资源的计划期供给量,如下表:
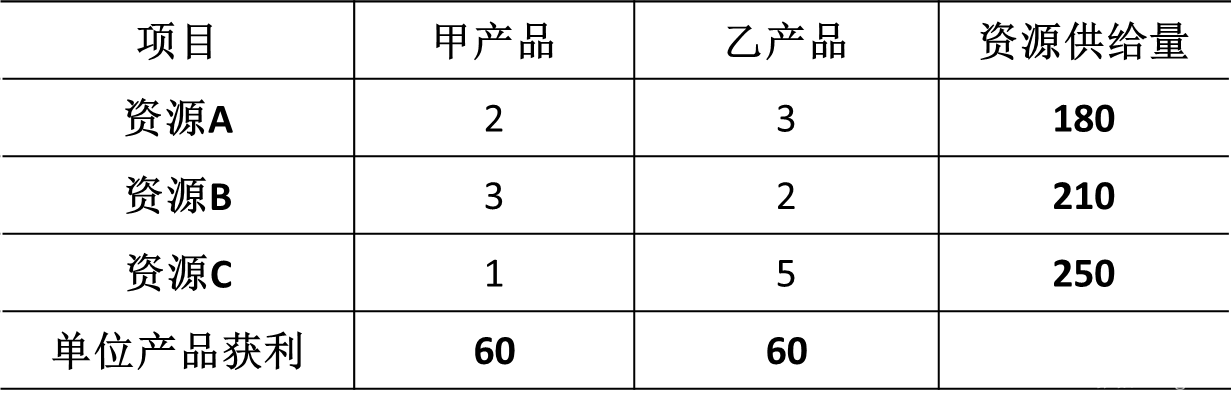 问题:工厂应分别生产多少单位甲、乙产品才能使工厂获利最多?
问题:工厂应分别生产多少单位甲、乙产品才能使工厂获利最多?
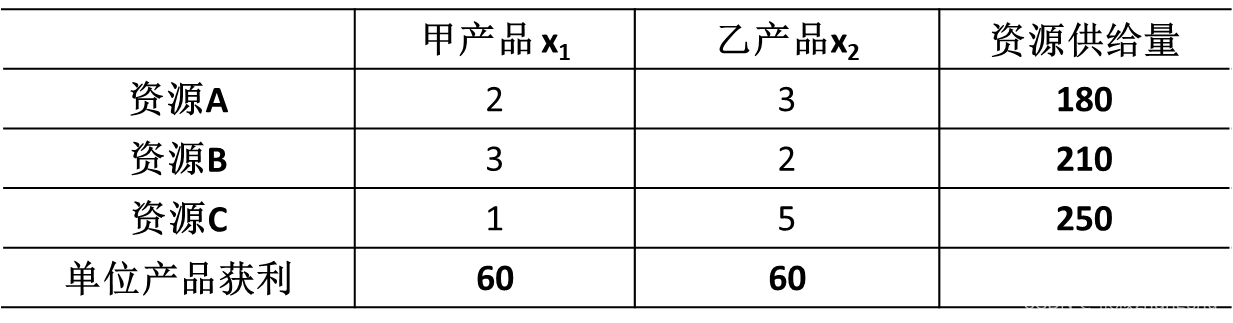
解:设 甲、乙产品的产量分别为x1、x2 ,
工厂获利为 z , 则
目标函数:
Max z = 60x1 + 60x2
约束条件:s.t.
2 x1 + 3 x2 ≤ 180
3 x1 + 2 x2 ≤ 210
x1 + 5 x2 ≤ 250
x1 , x2 ≥ 0
从上述的例子看出,建立数学模型的基本过程是:
1)搞清要解决的问题:目标 和 条件;
2)设置决策变量–描述解决问题的方案;
3)描述约束条件和非负约束;
4)给出目标函数,确定目标函数的优化方向,即优化是对目标函数取最大还是最小。
(2)线性规划模型:一般形式
目标函数:
Max(Min)z = c1 x1 + c2 x2 + … + cn xn
约束条件:s.t.
a11 x1 + a12 x2 + … + a1n xn ≤( =, ≥ )b1
a21 x1 + a22 x2 + … + a2n xn ≤( =, ≥ )b2
…… ……
am1 x1 + am2 x2 + … + amnxn ≤( =, ≥ )bm
x1 ,x2 ,… ,xn ≥ 0
线性规划一般数学模型的矩阵形式
目标函数 max(或min) z=c·x
约束条件 A·x≤ ( =, ≥ ) b
x≥0
式中 c=(c1,c2,…,cn), x=(x1,x2,…,xn)τ
a11 a12 … a1n
A= a21 a22 … a2n , b=(b1,b2,…,bm)τ… am1 am2 … amn
3)线性规划模型:标准形式
目标函数:
Max z = c1 x1 + c2 x2 + … + cn xn
约束条件:s.t.
a11 x1 + a12 x2 + … + a1n xn =b1
a21 x1 + a22 x2 + … + a2n xn =b2
…… ……
am1 x1 + am2 x2 + … + amnxn =bm
x1 ,x2 ,… ,xn ≥ 0
线性规划标准型的矩阵形式
目标函数 max z=c·x
约束条件 A·x = b
x≥0
式中 c=(c1,c2,…,cn), x=(x1,x2,…,xn)τ
a11 a12 … a1n
A= a21 a22 … a2n , b=(b1,b2,…,bm)τ… am1 am2 … amn
(4)线性规划的图解法
目标函数:
max Z= X1 + X2
约束条件:
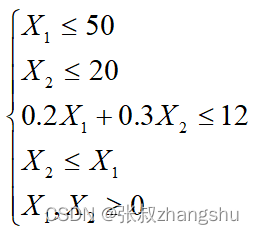
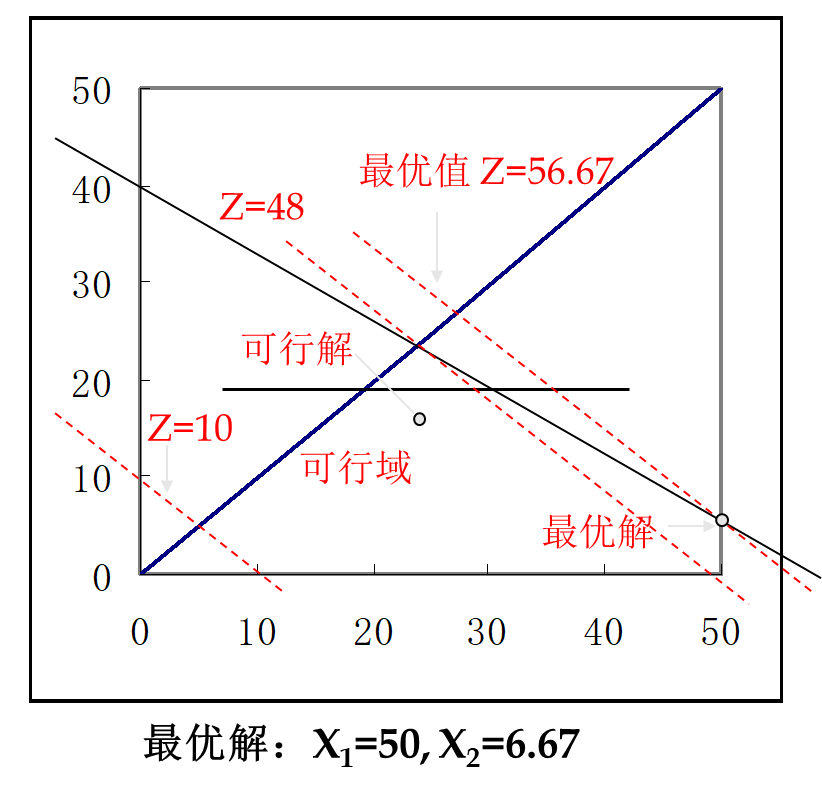
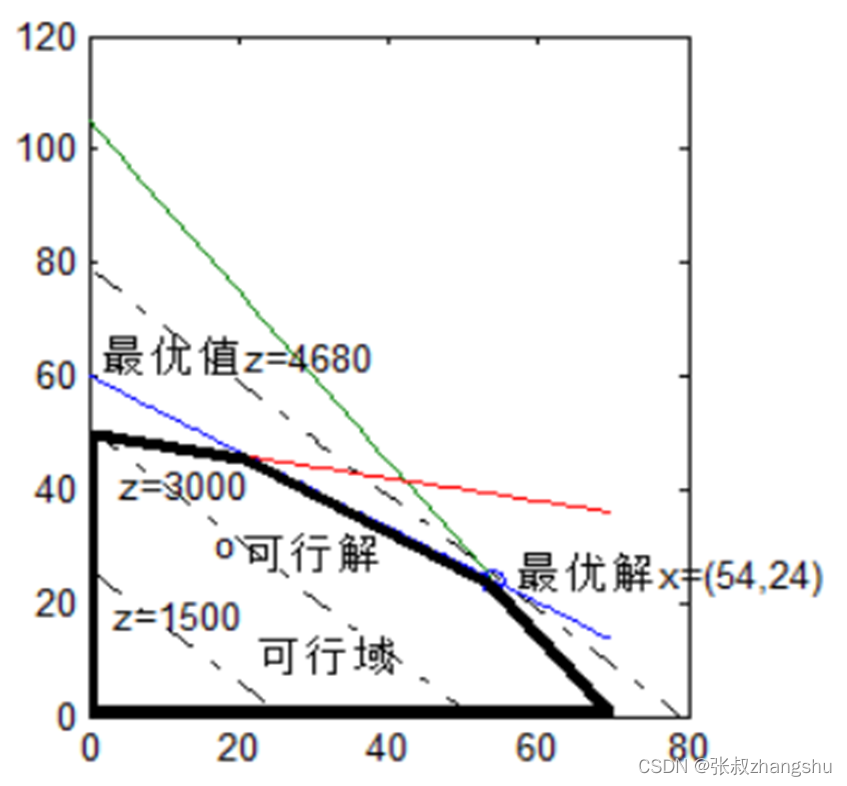
例1 的图解
目标函数:
Max z = 60 x1 + 60 x2
约束条件:
2 x1 + 3 x2 ≤ 180 (A)
3 x1 + 2 x2 ≤ 210 (B)
x1 + 5 x2 ≤ 250 ©
x1 , x2 ≥ 0 (D)
得到最优解:
x1 = 54, x2 = 24
最优目标值 z = 4680
解的几种情况:
线性规划的最优解如果存在
则必定有一个顶点(极点)是最优解
① 唯一解
目标函数等值线与约束边界只有一个交点
② 无穷多最优解
目标函数等值线与约束边界平行
③ 无界解
可行域不封闭
④ 无可行解
可行域为空集
(5)线性规划解的概念
引入松驰变量____含义是资源的剩余量
例1 中引入 s1, s2, s3 模型化为 标准型
目标函数:Max z = 60 x1 + 60 x2 + 0 s1 + 0 s2 + 0 s3
约束条件:s.t. 2 x1 + 3 x2 + s1 = 180
3 x1 + 2 x2 + s2 = 210
x1 + 5 x2 + s3 = 250
x1 , x2 , s1 , s2 , s3 ≥ 0
对于标准型的最优解 x1 =54 x2 = 24 , s1 = 0 s2 = 0 s3 = 76
说明:生产54单位甲产品和24单位乙产品将消耗完所有的A、B资源,但对资源C则还剩余76。
基最优解、最优解、基可行解、基解、可行解的关系如下所示:

(6)线性规划的基本定理
① 线性规划问题的所有可行解构成的集合(可行域)
R={x|A·x=b,x≥0}
R是一凸集(包括无界域),它有有限个顶点;
② 线性规划问题的每个基可行解
对应可行域凸集R的一个顶点;
③ 若线性规划问题有最优解,
则必定在某顶点处得到
基本定理把可行域的有限个顶点与基可行解这一代数概念联系起来,可通过求基可行解的代数方法来得到可行域的一切极点,能在有限的计算中获得最优点。
