站长交易网全网整合营销

104. 二叉树的最大深度

题目

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例：

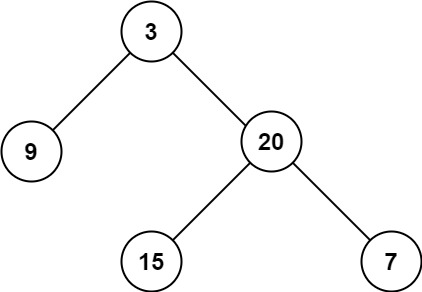
输入：root = [3,9,20,null,null,15,7]
输出：3

思路

用递归来做，其中心思路是，一个结点的最大深度相当于其左右子树的最大深度加一，这就可以利用递归求得子树深度了。

接下来是递归三部曲：

1. 首先确定返回值和参数，返回值肯定是深度，参数则是二叉树结点；

2. 其次确定递归终止条件，也就是当结点为空时返回0；

3. 最后明确每一次递归要做的事，其实就是按找中心思路返回最大深度。

代码

class Solution {
public:int getdepth(TreeNode* node) {if (node == NULL) return 0;int leftdepth = getdepth(node->left);int rightdepth = getdepth(node->right);int depth = 1 + max(leftdepth, rightdepth);return depth;}int maxDepth(TreeNode* root) {return getdepth(root);}
};

111. 二叉树的最小深度

题目

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

思路

这道题的中心思路跟上面的一样，都是用递归法，每次取左右子树最小深度加一，不过这里有一个易错点，那就是深度要从叶子结点开始算，所以当遇到一个只有一个子树的结点时，不能记录空的一边，而是递归返回有子树的那边的深度。

代码

class Solution {
public:int getdepth(TreeNode* node) {if (node == NULL) return 0;int leftdepth = getdepth(node->left);int rightdepth = getdepth(node->right);if (node->left == NULL && node->right != NULL)return 1 + rightdepth;if (node->left != NULL && node->right == NULL)return 1 + leftdepth;int depth = 1 + min(leftdepth, rightdepth);return depth;}int minDepth(TreeNode* root) {return getdepth(root); }
};

222. 完全二叉树的结点个数

题目

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

普通解法

管他完不完全，反正也是二叉树，既然是二叉树，之前学过的递归和非递归遍历都可以用来求结点数，只需要把原来的结点值入vector变成计数器加一，下面是用非递归前序遍历来做的：

class Solution {
public:int countNodes(TreeNode* root) {stack<TreeNode*> st;int num = 0;if (root != NULL) st.push(root);while (!st.empty()) {TreeNode* cur = st.top();st.pop();num++;if (cur->right) st.push(cur->right);if (cur->left) st.push(cur->left);}return num;}
};

完全二叉树解法

完全二叉树可以不断拆分为一个满二叉树和一个完全二叉树，每一个满二叉树可以一边往下走一边求深度，如果左右子树的深度相同，就可以直接计算出这个二叉树的结点个数，因为满二叉树的结点数等于2的深度次方减一，如果不是满二叉树，就递归求解这个完全二叉树的根节点的左右子树的结点数再加一。

class Solution {
public:int countNodes(TreeNode* root) {if (root == NULL) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int leftDepth = 0, rightDepth = 0;while (left) {left = left->left;leftDepth++;}while (right) {right = right->right;rightDepth++;}if (leftDepth == rightDepth) {return (2 << leftDepth) - 1;}return countNodes(root->left) + countNodes(root->right) + 1;}
};