大型网站开发项目书籍网站首页关键词如何优化
差分约束
差分约束系统包含 m m m个涉及 n n n个变量的差额限制条件,这些差额限制条件每个都是形式为 x i − x j ≤ b ∈ [ 1 , m ] x_i-x_j\leq b_{\in[1,m]} xi−xj≤b∈[1,m]的简单线性不等式。
通常我们要求解出一组可行解。
最短路差分约束
如果我们把变量看做节点,如果这里用 d u d_u du表示 d i s S , u dis_{S,u} disS,u,那么从 u u u到 v v v的一条有向边必然满足 d u + w ≥ d v d_u+w\geq d_v du+w≥dv,即:
d v − d u ≤ w d_v-d_u\leq w dv−du≤w
对比:
x v − x u ≤ b i x_v-x_u\leq b_i xv−xu≤bi
因此对于每个限制条件 x v − x u ≤ b i x_v-x_u\leq b_i xv−xu≤bi,我们可以在图上给 u u u到 v v v连接一条边权为 b i b_i bi的有向边。
同时建立一个虚拟源点 S S S,向着每个点连接一个长度为 0 0 0的边。
如果图中不存在负环,那么可以使用单源最短路径算法求出所有的 d u d_u du,则 x i = d i x_i=d_i xi=di就是原问题的一组可行解。如果有负环说明无解。
定理:图中没有负环是差分约束系统有解的充要条件。
充分性显然,因为我们可以构造出一组解。
必要性:
如果图中存在负环,那么说明此差分约束系统无解:
设图中有一个负环, w 1 + w 2 + w 3 < 0 w_1+w_2+w_3<0 w1+w2+w3<0
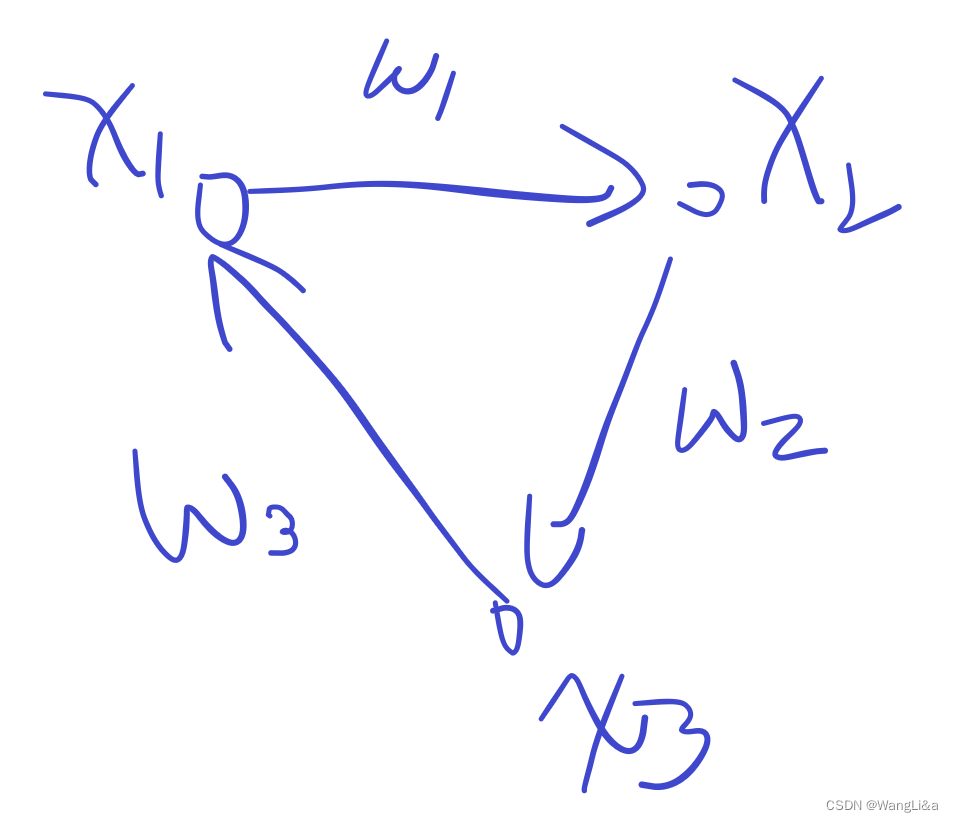
x 1 + w 1 ≥ x 2 x_1+w_1\geq x_2 x1+w1≥x2
x 1 + w 1 + w 2 ≥ x 2 + w 2 ≥ x 3 x_1+w_1+w_2\geq x_2+w_2\geq x_3 x1+w1+w2≥x2+w2≥x3
x 1 + w 1 + w 2 + w 3 ≥ x 3 + w 3 ≥ x 1 x_1+w_1+w_2+w_3 \geq x_3+w_3\geq x_1 x1+w1+w2+w3≥x3+w3≥x1
x 1 + w 1 + w 2 + w 3 ≥ x 1 x_1+w_1+w_2+w_3 \geq x_1 x1+w1+w2+w3≥x1
这说明 x 1 + 一个负数 ≥ x 1 x_1+一个负数\geq x_1 x1+一个负数≥x1,这是不可能的,因此这个差分约束系统是矛盾的,无解。
QED.
性质
这样建图跑最短路求出的解是具有一定性质的,具体来说是:
- x i ∈ [ 1 , n ] ≤ 0 x_{i\in[1,n]}\leq 0 xi∈[1,n]≤0
- 对于任意差分约束系统的一组解 { x n ′ } \left\{x'_{n}\right\} {xn′}满足 x i ∈ [ 1 , n ] ′ ≤ 0 x'_{i\in[1,n]}\leq 0 xi∈[1,n]′≤0,都有 x i ≥ x i ′ ( i ∈ [ 1 , n ] ) x_i\geq x'_i(i\in[1,n]) xi≥xi′(i∈[1,n]),也就称为最大解
- 对于所有解 x i ∈ [ 1 , n ] ′ ≤ 0 x'_{i\in[1,n]}\leq 0 xi∈[1,n]′≤0,都有 ∑ n i = 1 x i ≥ ∑ n i = 1 x i ′ \underset{i=1}{\overset n\sum}x_i\geq\underset{i=1}{\overset n\sum}x'_i i=1∑nxi≥i=1∑nxi′
证明:
只需证明性质2,性质1、3显然:
首先考虑虚拟源点 S S S的意义,即我们令 x S x_S xS表示一个新量,我们连零边表示: x i ∈ [ 1 , n ] − x S ≤ 0 x_{i\in[1,n]}-x_S\leq 0 xi∈[1,n]−xS≤0。
然后我们在跑最短路时强制 x S = d S = 0 x_S=d_S=0 xS=dS=0,因此我们连零边实际上限制了: x i ∈ [ 1 , n ] ≤ 0 x_{i\in[1,n]}\leq 0 xi∈[1,n]≤0
接下来考虑:
对于 x i = d i x_i=d_i xi=di,假设其对应的某条从 S S S到 i i i的最短路径依次经过了点 u 0 = S , u 1 , u 2 , . . . , u k = i u_0=S,u_1,u_2,...,u_k=i u0=S,u1,u2,...,uk=i,则经过的边对应的不等式为:
x u j − x u j − 1 ≤ w j x_{u_j}-x_{u_{j-1}}\leq w_j xuj−xuj−1≤wj
求和得到:
∑ k j = 1 x u j − x u j − 1 ≤ ∑ k j = 1 w j \underset{j=1}{\overset k\sum}x_{u_j}-x_{u_{j-1}}\leq \underset{j=1}{\overset k\sum} w_j j=1∑kxuj−xuj−1≤j=1∑kwj
由于裂项:
x u k − x u 0 ≤ ∑ k j = 1 w j x_{u_k}-x_{u_0}\leq \underset{j=1}{\overset k\sum}w_j xuk−xu0≤j=1∑kwj
由于我们指定了 x S = 0 x_S=0 xS=0,也就是说:
x i ≤ ∑ k j = 1 w j x_i\leq \underset{j=1}{\overset k\sum}w_j xi≤j=1∑kwj
这给出了此差分约束系统中,满足所有变量都 ≤ 0 \leq 0 ≤0的任意一个解中, x i x_i xi的一个上界。
同时我们断言这个上界是可以取到的,并且 x i = d i = ∑ k j = 1 w j x_i=d_{i}=\underset{j=1}{\overset k\sum}w_j xi=di=j=1∑kwj,原因如下,因为刚才经过的边事实上是由 S S S到 i i i的最短路径,根据相关理论,我们有:
d i s S , u j − d i s S , u j − 1 = w j dis_{S,u_j}-dis_{S,u_{j-1}}=w_j disS,uj−disS,uj−1=wj
求和得到:
∑ k j = 1 d i s S , u j − d i s S , u j − 1 = ∑ k j = 1 w j \underset{j=1}{\overset k\sum}dis_{S,u_j}-dis_{S,u_{j-1}}= \underset{j=1}{\overset k\sum} w_j j=1∑kdisS,uj−disS,uj−1=j=1∑kwj
由于裂项:
d i s S , i = ∑ k j = 1 w j dis_{S,i}=\underset{j=1}{\overset k\sum}w_j disS,i=j=1∑kwj
因此我们知道 x i = d i = d i s S , i = ∑ k j = 1 w j x_i=d_i=dis_{S,i}=\underset{j=1}{\overset k\sum}w_j xi=di=disS,i=j=1∑kwj,证明上界可以取到。
QED.
最长路差分约束
如果我们用 d u d_u du表示 S S S到 u u u的最长路,那么对于有向边 ( u , v ) (u,v) (u,v):
d u + w ≤ d v d_u+w\leq d_v du+w≤dv
d u − d v ≤ − w d_u-d_v\leq -w du−dv≤−w
即:
x u − x v ≤ b i x_u-x_v\leq b_i xu−xv≤bi
那么 b i = − w b_i=-w bi=−w,即 w = − b i w=-b_i w=−bi
那么从 u u u向 v v v连接一条长度为 − b i -b_i −bi的有向边。
在从虚拟源点 S S S向着每个点连接一个边权为 0 0 0的有向边。
求出图中的最长路即为差分约束系统的一组解。
同理图中如果存在正环就无解。
性质
这样建图跑最长路求出的解也具有一定性质的,具体来说是:
- x i ∈ [ 1 , n ] ≥ 0 x_{i\in[1,n]}\geq 0 xi∈[1,n]≥0
- 对于任意差分约束系统的一组解 { x n ′ } \left\{x'_{n}\right\} {xn′}满足 x i ∈ [ 1 , n ] ′ ≥ 0 x'_{i\in[1,n]}\geq 0 xi∈[1,n]′≥0,都有 x i ≤ x i ′ ( i ∈ [ 1 , n ] ) x_i\leq x'_i(i\in[1,n]) xi≤xi′(i∈[1,n]),也就称为最小解
- 对于所有解 x i ∈ [ 1 , n ] ′ ≥ 0 x'_{i\in[1,n]}\geq 0 xi∈[1,n]′≥0,都有 ∑ n i = 1 x i ≤ ∑ n i = 1 x i ′ \underset{i=1}{\overset n\sum}x_i\leq\underset{i=1}{\overset n\sum}x'_i i=1∑nxi≤i=1∑nxi′
证明同理。
其他问题
各类限制转化
通常讨论的差分约束问题往往变量为整数,对于一些其他形式的简单线性不等式可以转化为差分约束问题 x − y ≤ b x-y\leq b x−y≤b:
x − y < b ⇒ x − y ≤ b − 1 x-y<b\Rightarrow x-y\leq b-1 x−y<b⇒x−y≤b−1
x − y ≥ b ⇒ y − x ≤ − b x-y\geq b\Rightarrow y-x\leq -b x−y≥b⇒y−x≤−b
x − y > b ⇒ y − x < − b x-y>b\Rightarrow y-x<-b x−y>b⇒y−x<−b
x − y = b ⇒ x − y ≤ b 且 x − y ≥ b x-y=b\Rightarrow x-y\leq b且x-y\geq b x−y=b⇒x−y≤b且x−y≥b(当然如果全是等式限制直接高斯消元更好)
通常差分约束可能涉及对题意进行差分/前缀和转化。
正解/负解
建最短路得出的解一定是非正解,并且是最大解。
建最长路得出的解一定是非负解,并且是最小解。
同时注意到对一组可行解的每个变量都加 k k k之后,这个解仍然是可行解,因此我们可以获得全正/全负解。
后记
于是皆大欢喜。
