怎么做黄网站自己如何制作一个小程序
参考资料:
【【零基础入门量子计算-第03讲】线性代数初步与复数】
来自b站up:溴锑锑跃迁
建议关注他的更多高质量文章:CSDN:【溴锑锑跃迁】
0. 前言
强烈建议搭配b站原视频进行观看,这只是我当时看的笔记,读懂这堂课的内容可能需要:线性代数(初等变换、列向量)、离散数学(群)、高等数学(极限等价无穷小部分)的知识储备
1. 向量的表示与运算
-
平面向量基本定理,可推广至三维或更多维度情况
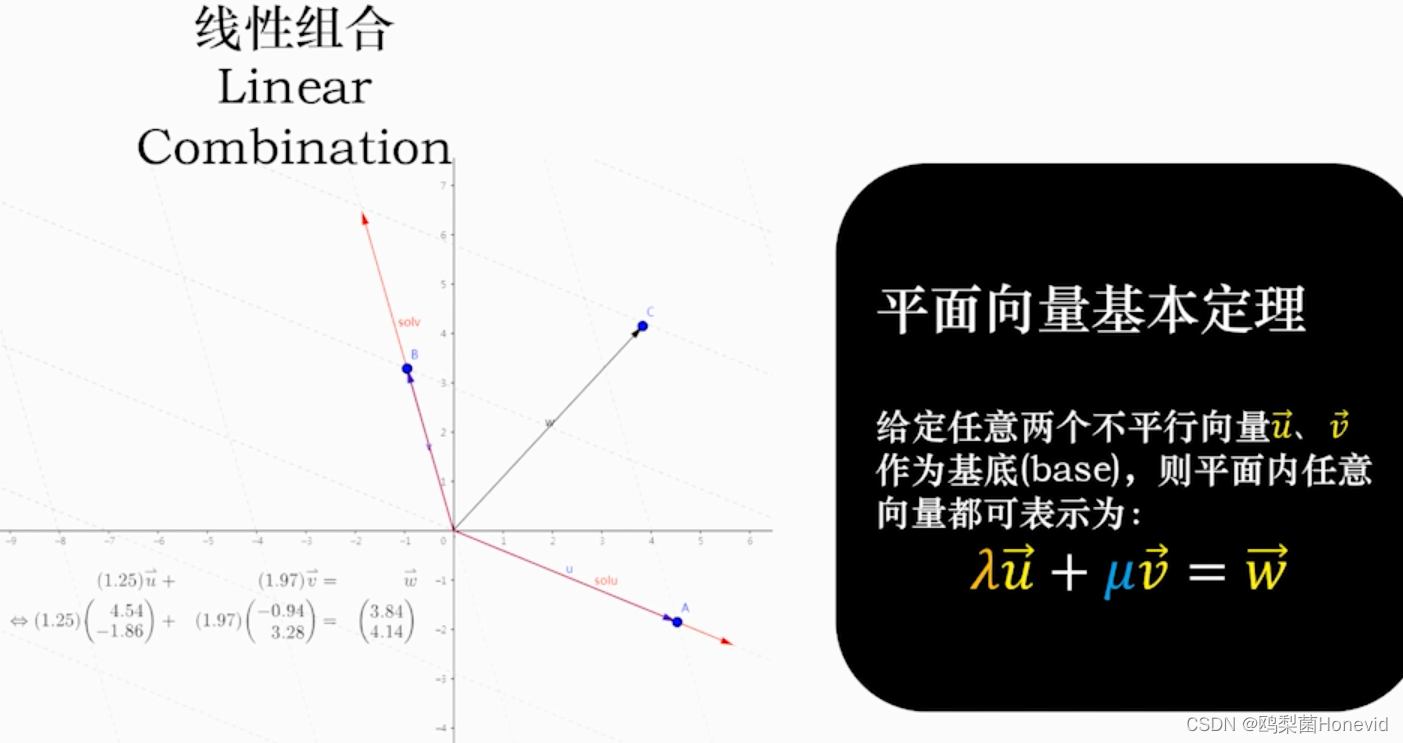
-
内积=点乘,得到标量
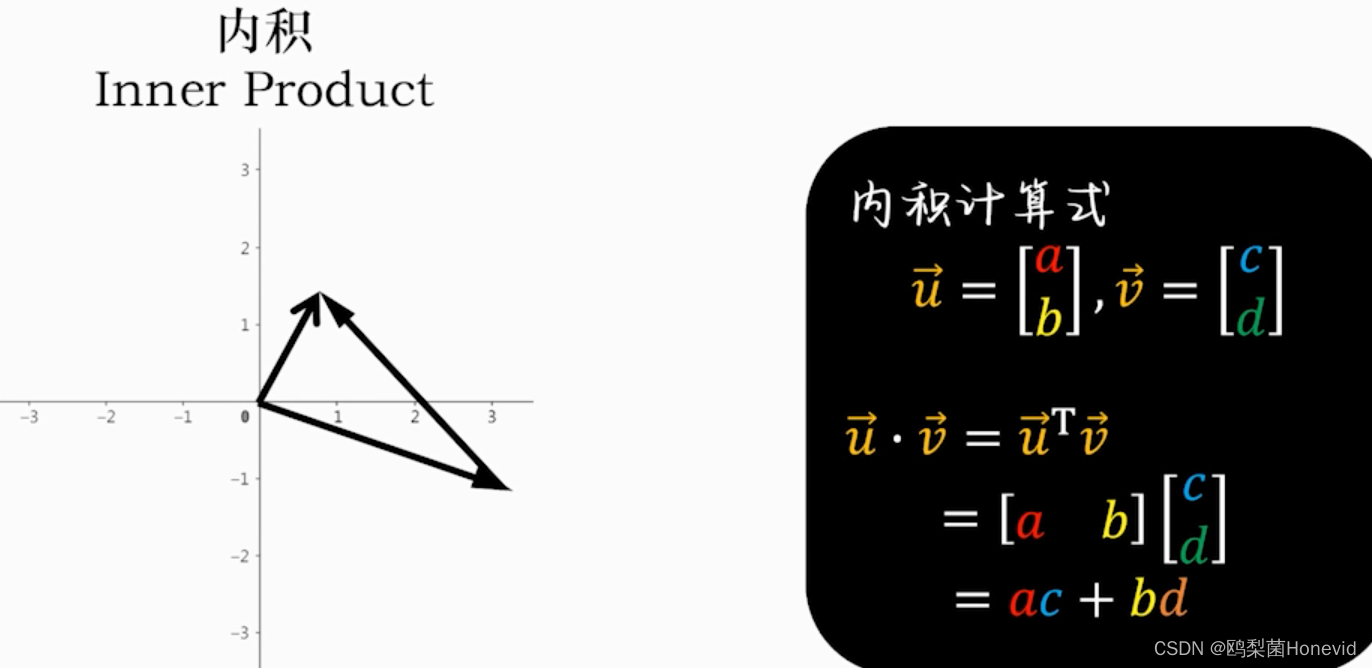
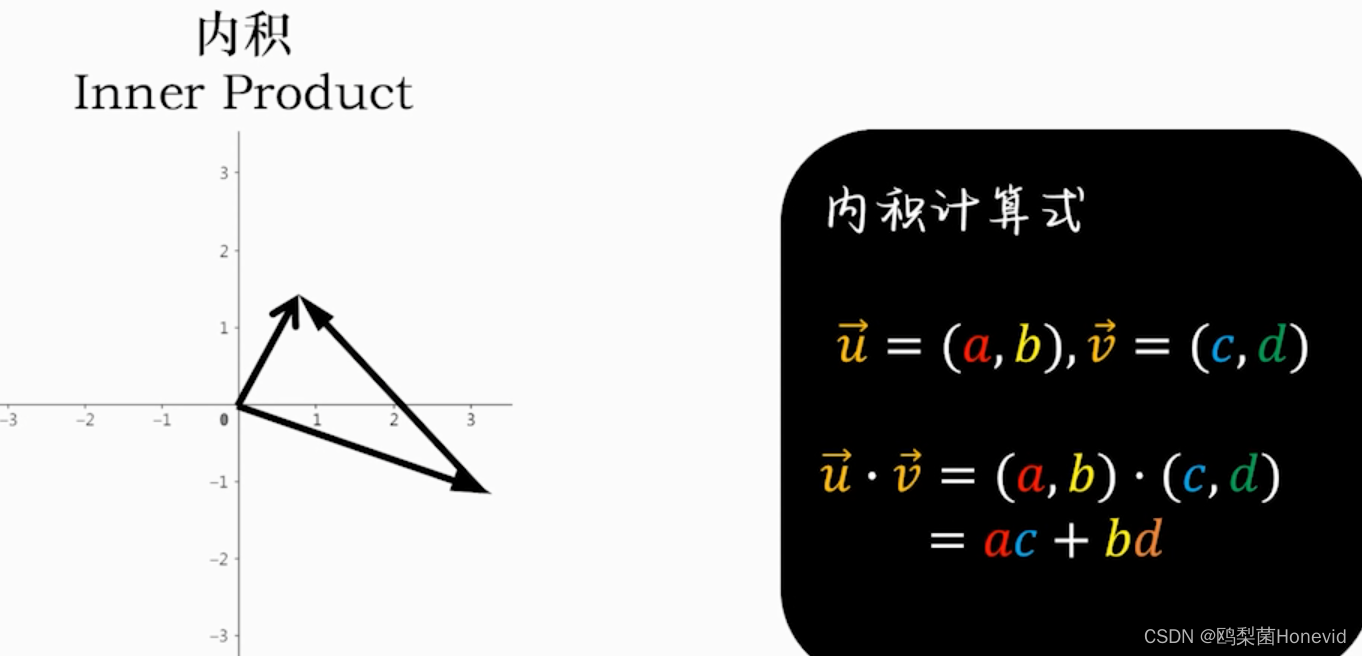
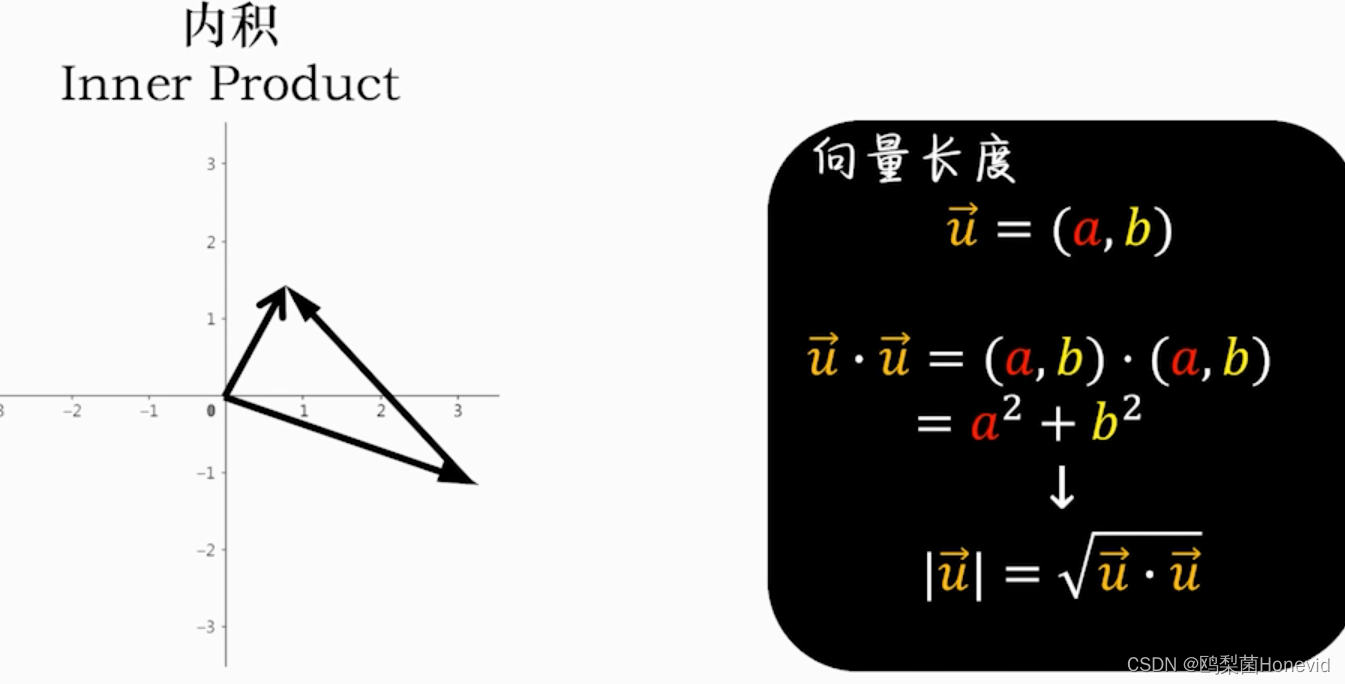
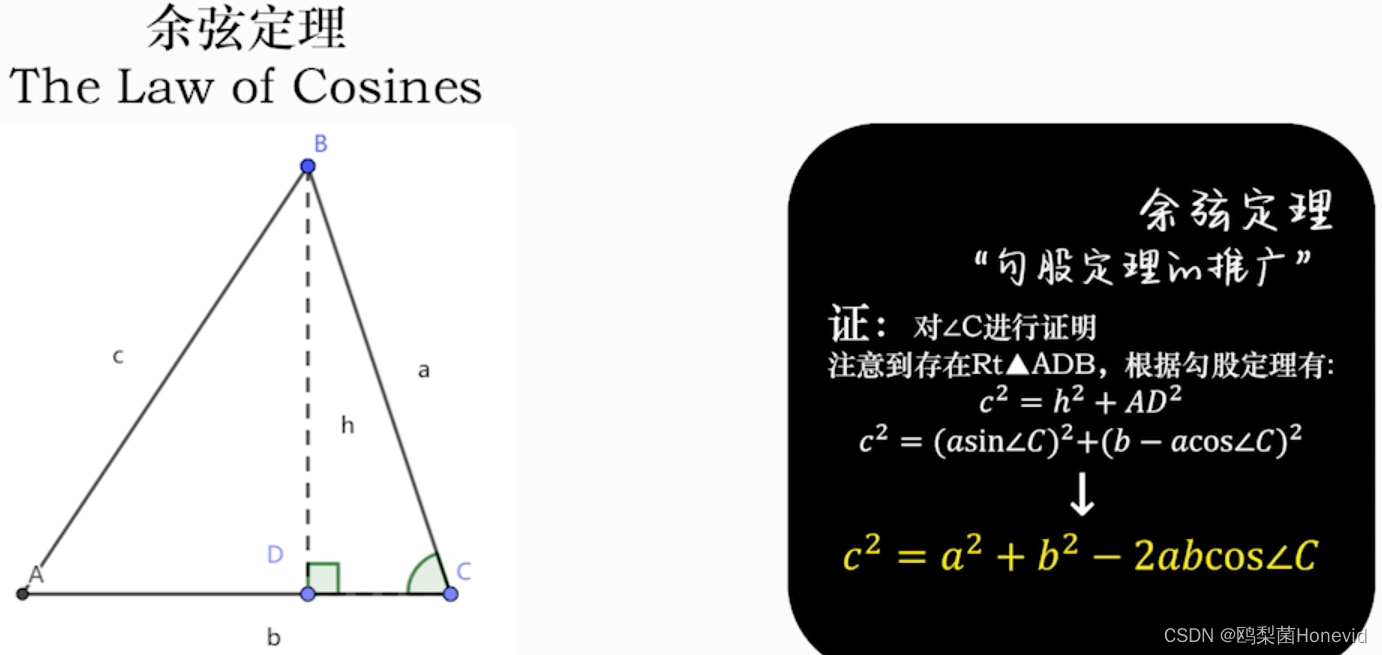
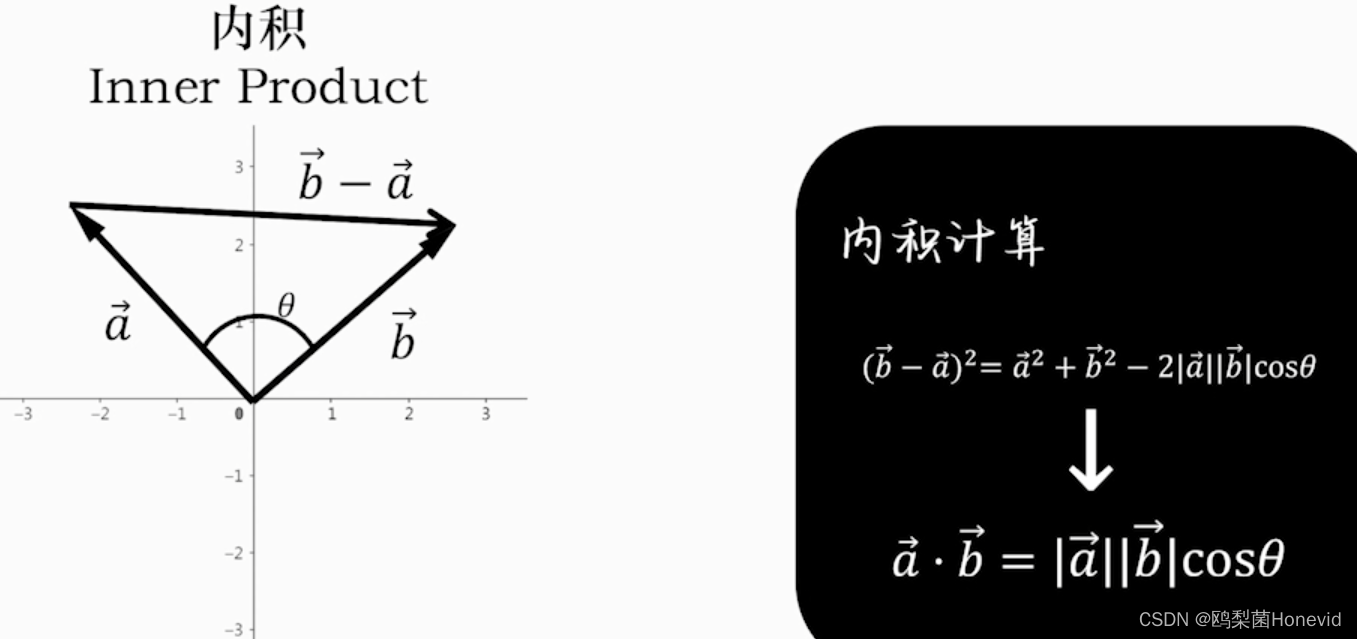
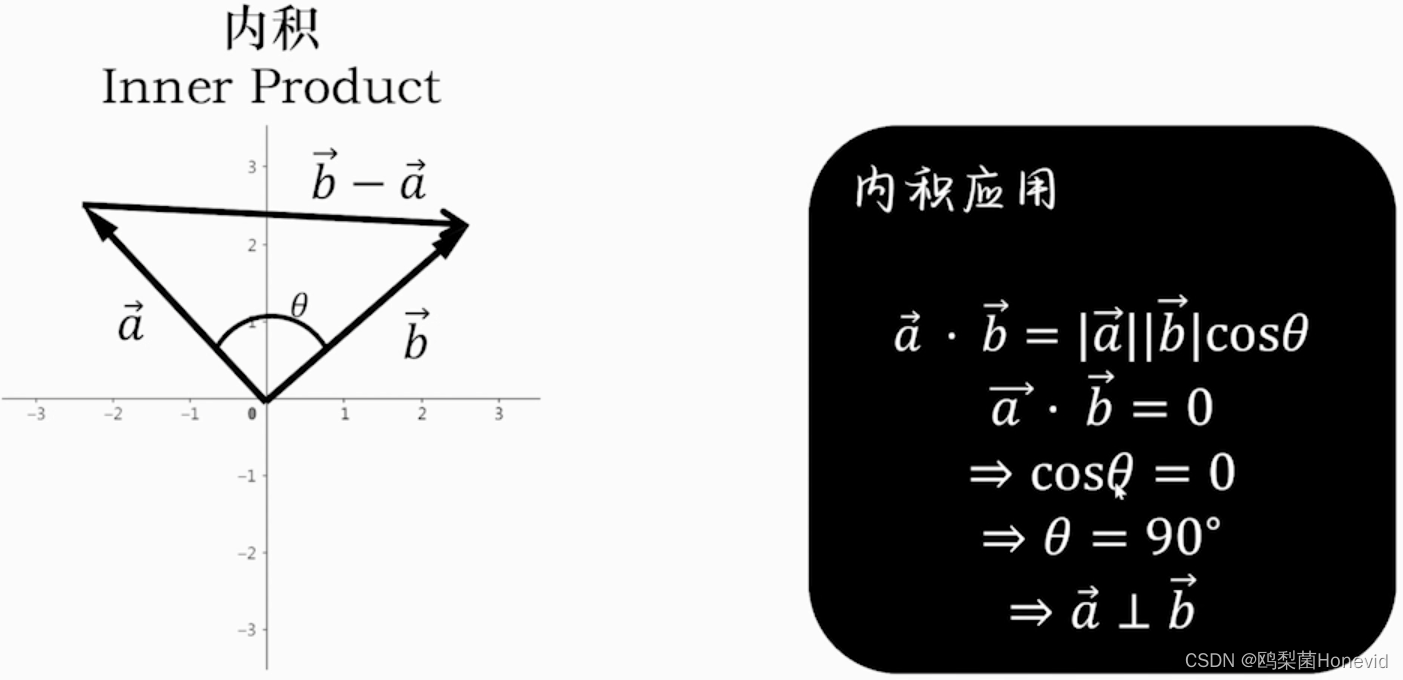
-
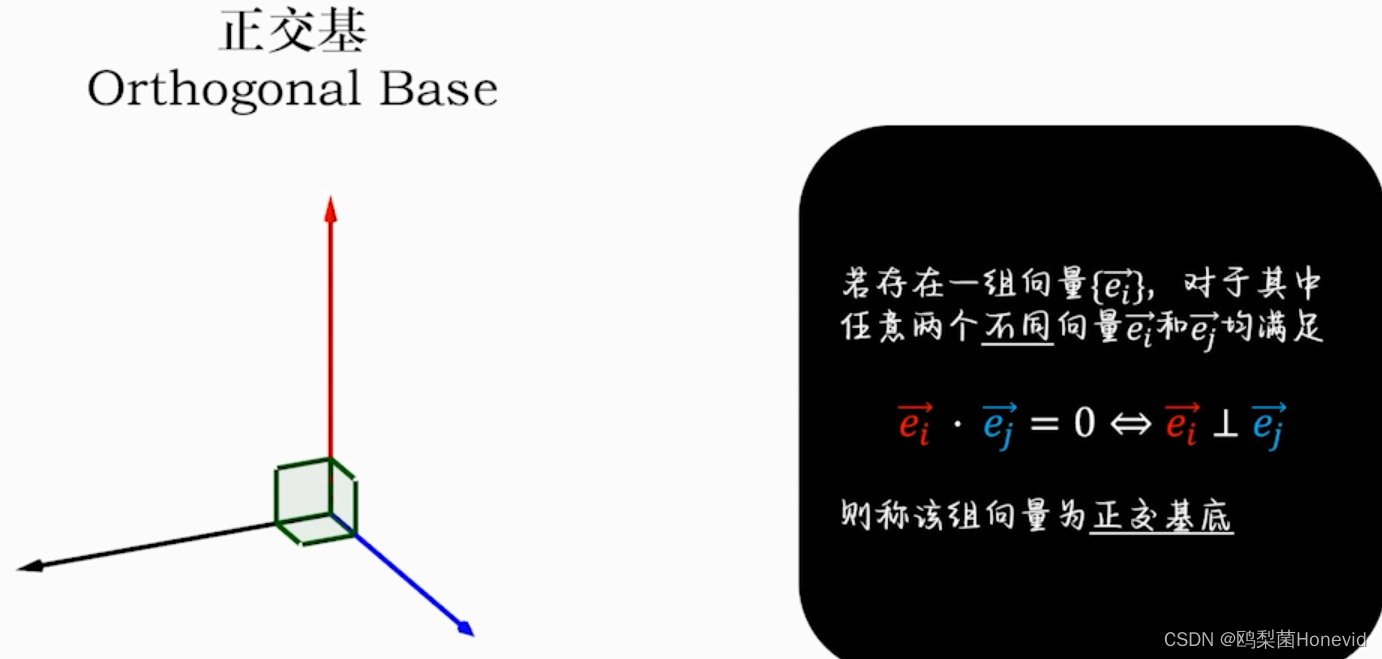
正交基——内积为零的两向量相互垂直,称为正交基底


2. 矩阵表示及其运算


-
矩阵运算法则
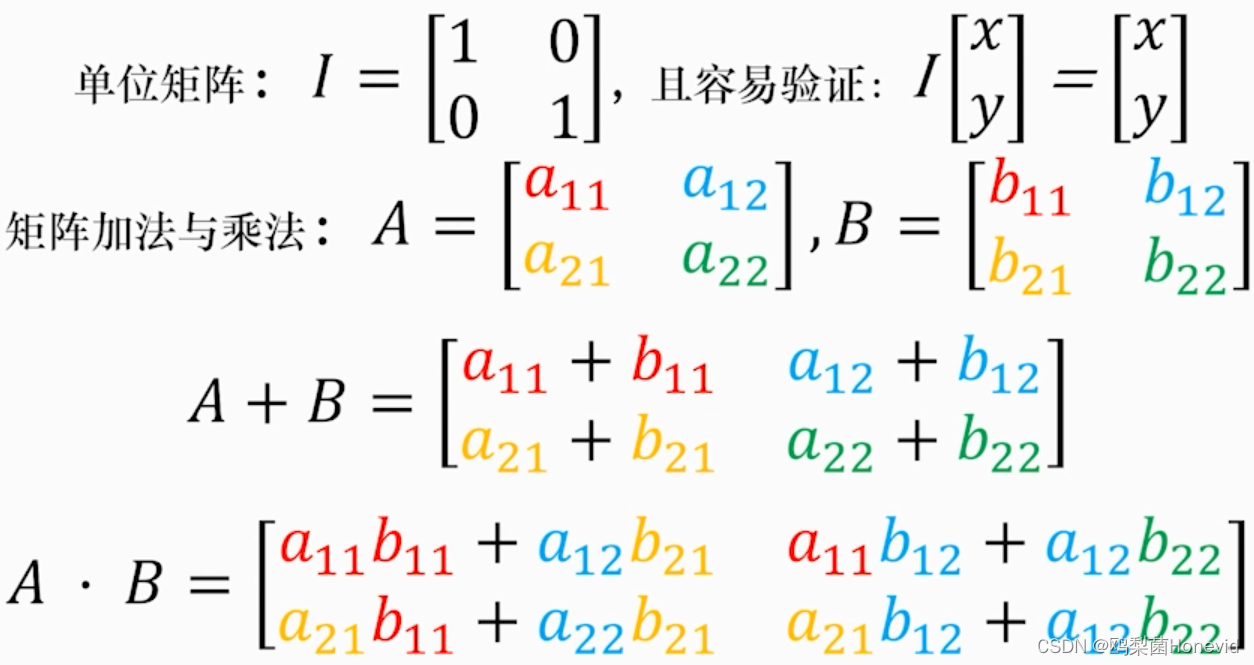

-
矩阵初等变换

-
逆矩阵(up的视频里面这里要是有如下文字提示可能会更好)
设有矩阵 A A A和矩阵 B B B,有 A B = E AB=E AB=E(其中 E E E表示为单位矩阵,有的地方会用 I I I表示),则B为A的逆矩阵,即有 B = A − 1 B=A^{-1} B=A−1
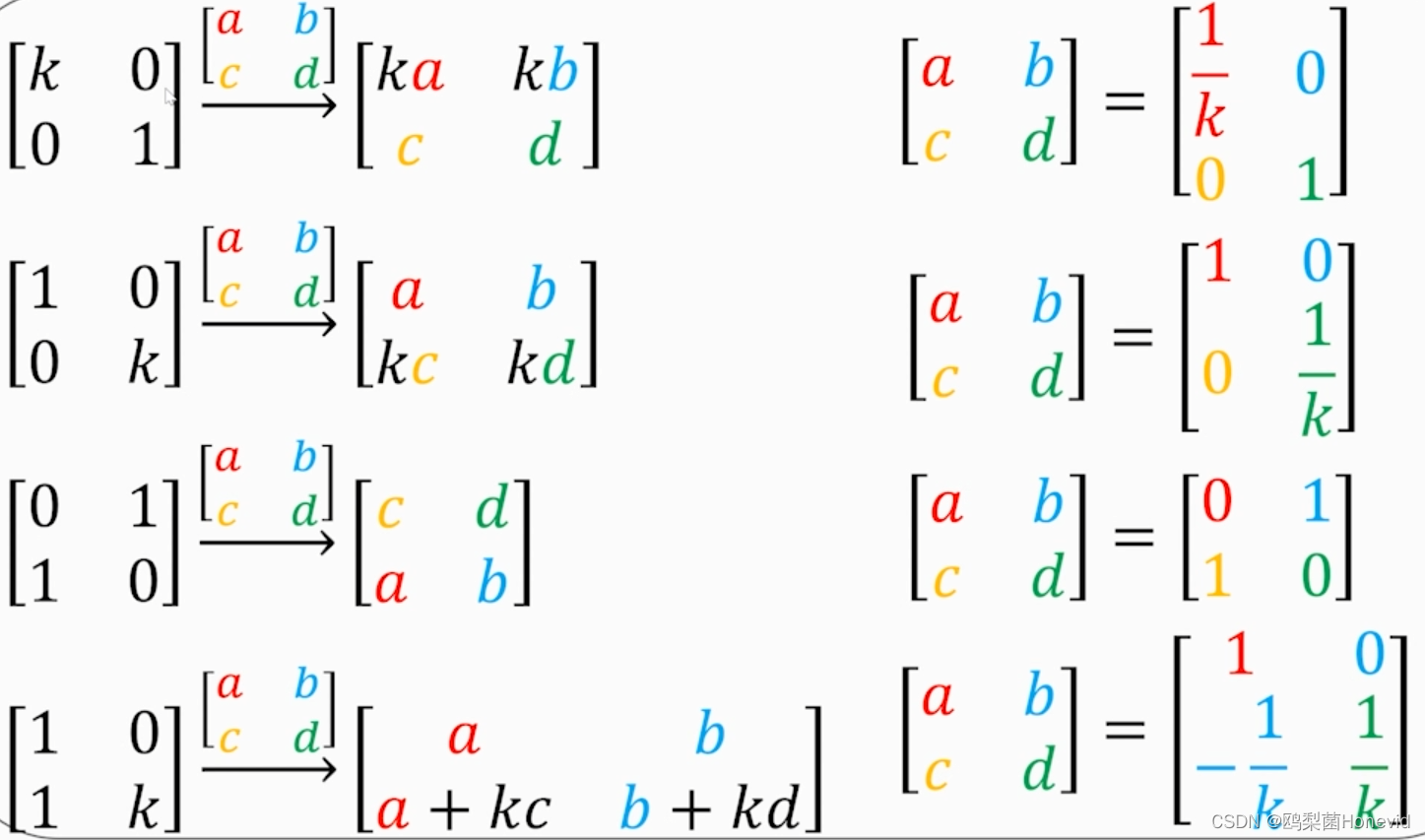
对之前鸡兔同笼所列矩阵求解过程进行详细展示,关键是求逆矩阵左乘到右侧



矩阵等式的理解方式


- 理解方式一:(上图左)映射、矩阵变换,即从一个向量向另一个向量变换=矩阵
- 理解方式二:(上图右)用坐标系本身代表的基底去组合成新的向量


旋转矩阵:





3. 群的简介(离散数学相关)
1. 群的定义
-
考虑一个集合G并对其中元素定义/指定一种操作称为群乘法
-
集合G在指定群乘法后其中元素应当满足以下四条性质才能被称作群
-
封闭性

-
结合律

-
单位元

-
逆元素

 日是e的象形
日是e的象形


下面上三个实例



同态映射:先作用再乘法=先乘法再作用

即: e x ∗ e y = e x + y e^x*e^y=e^{x+y} ex∗ey=ex+y,即 f ( x ) + f ( y ) = f ( x + y ) f(x)+f(y)=f(x+y) f(x)+f(y)=f(x+y) -

4. 复数简介


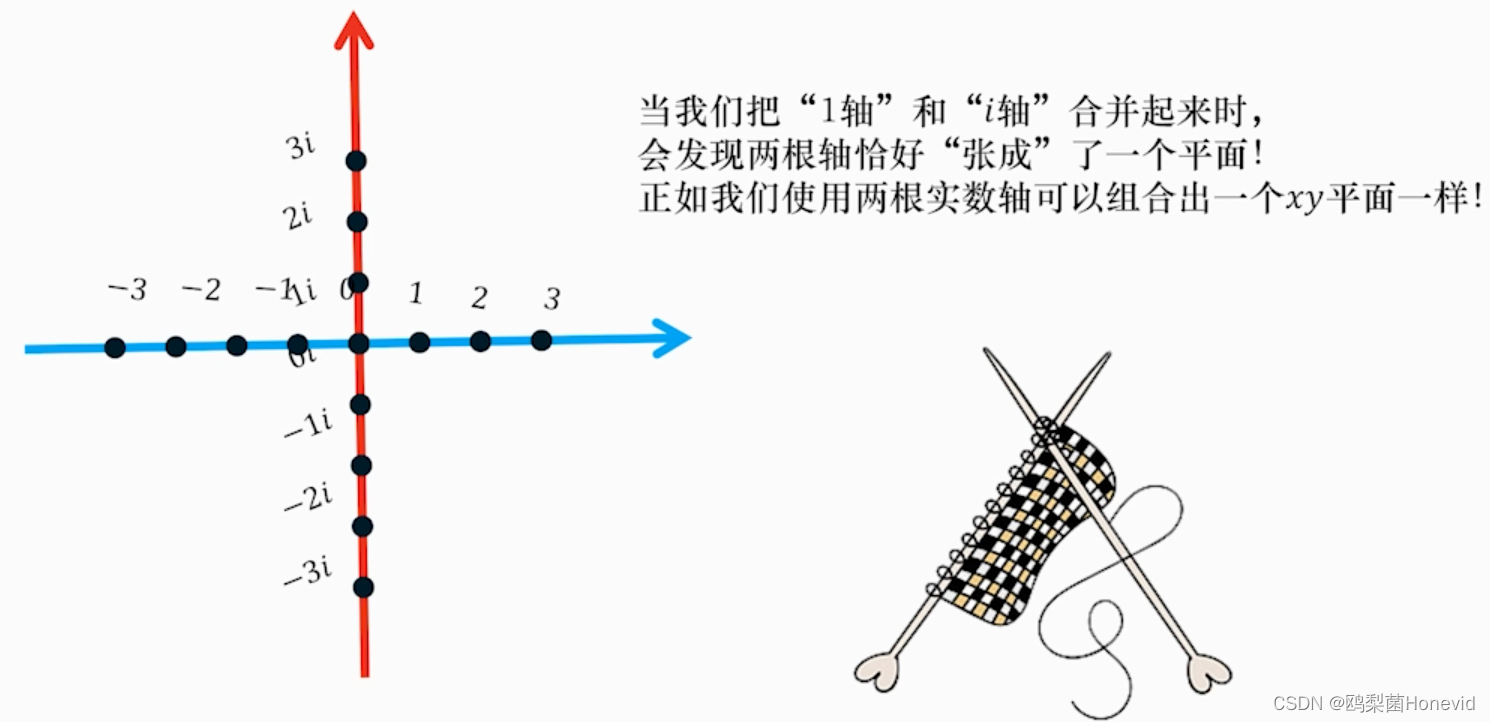
i轴和1轴的0处是同一个0,将他们连接起来构成一个平面!!!

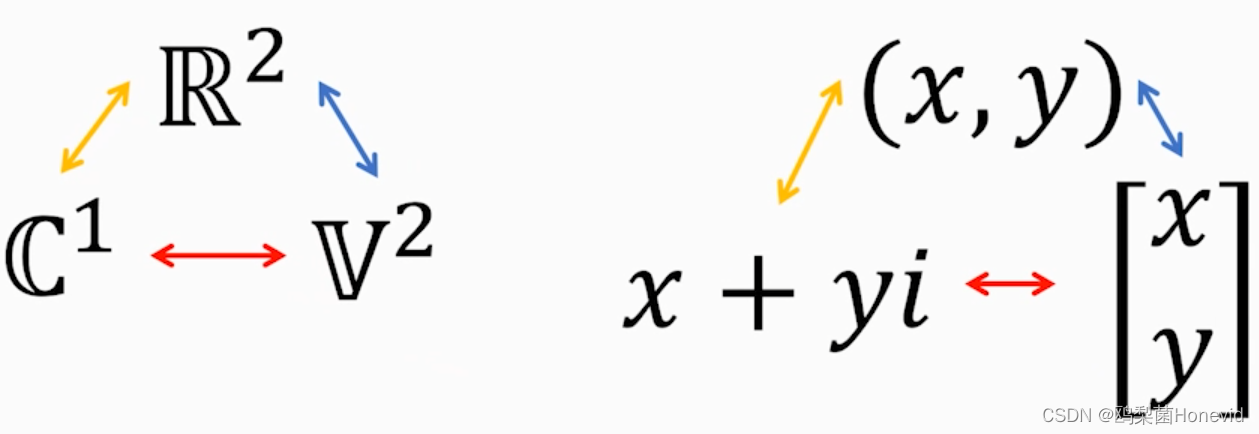
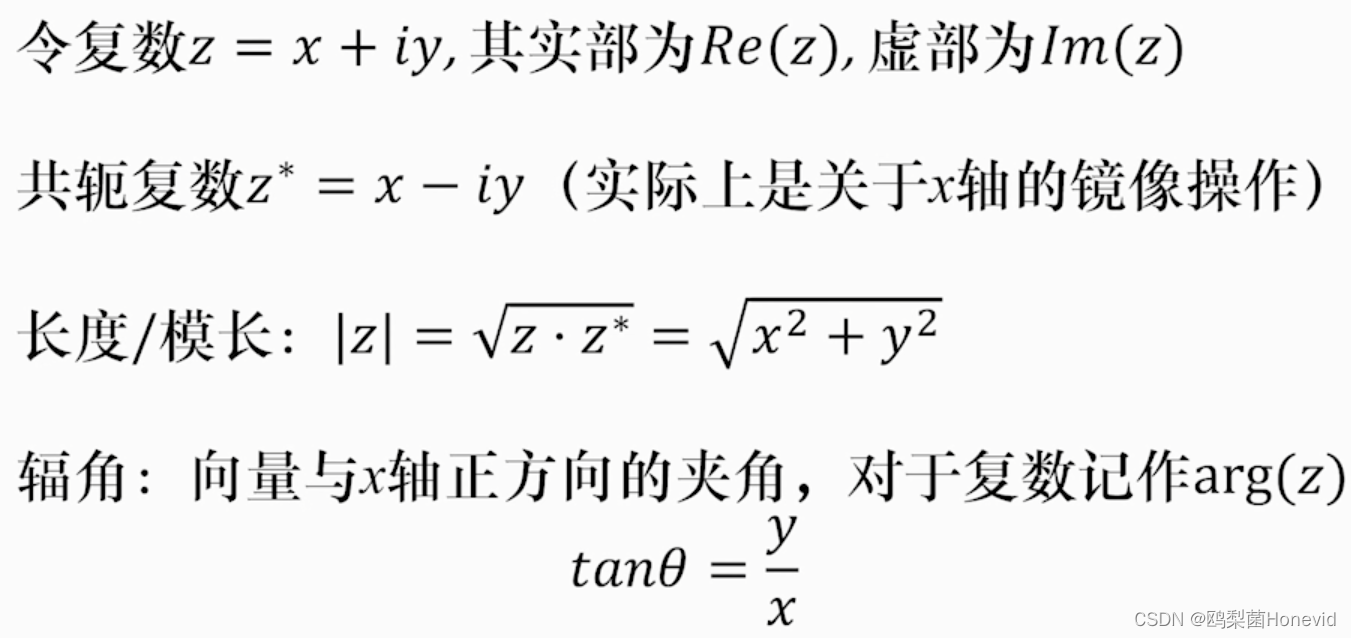
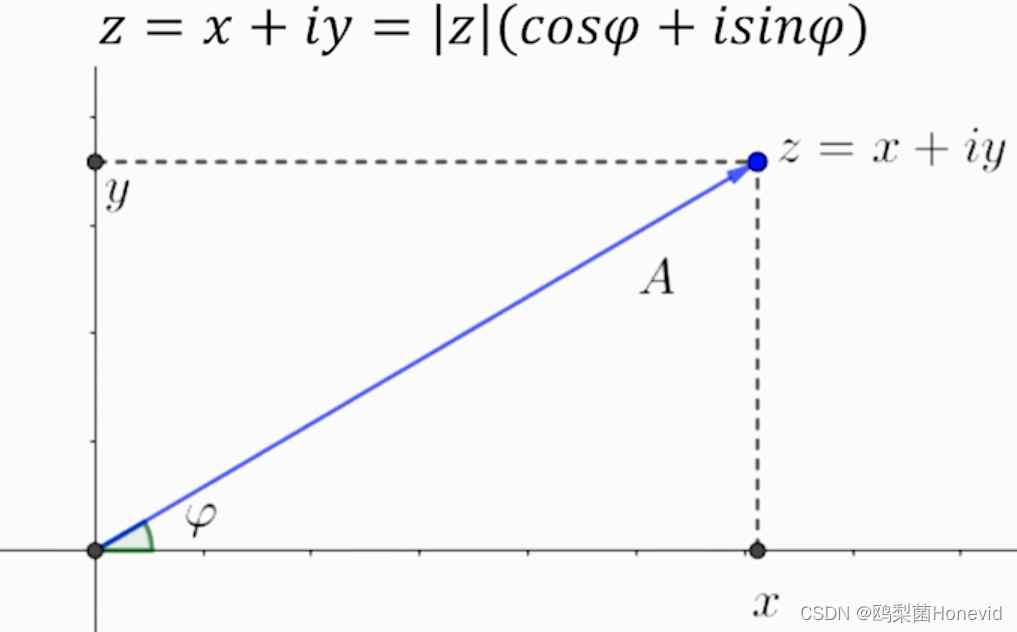
平面上表示
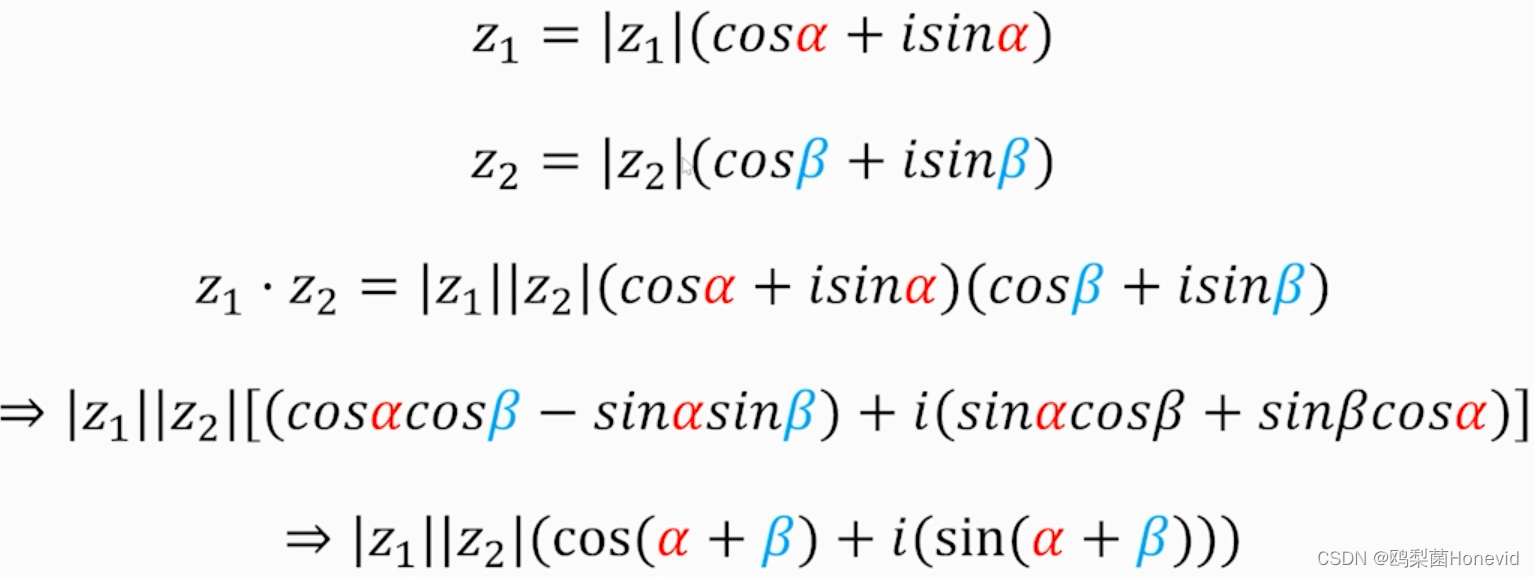
棣莫弗定理

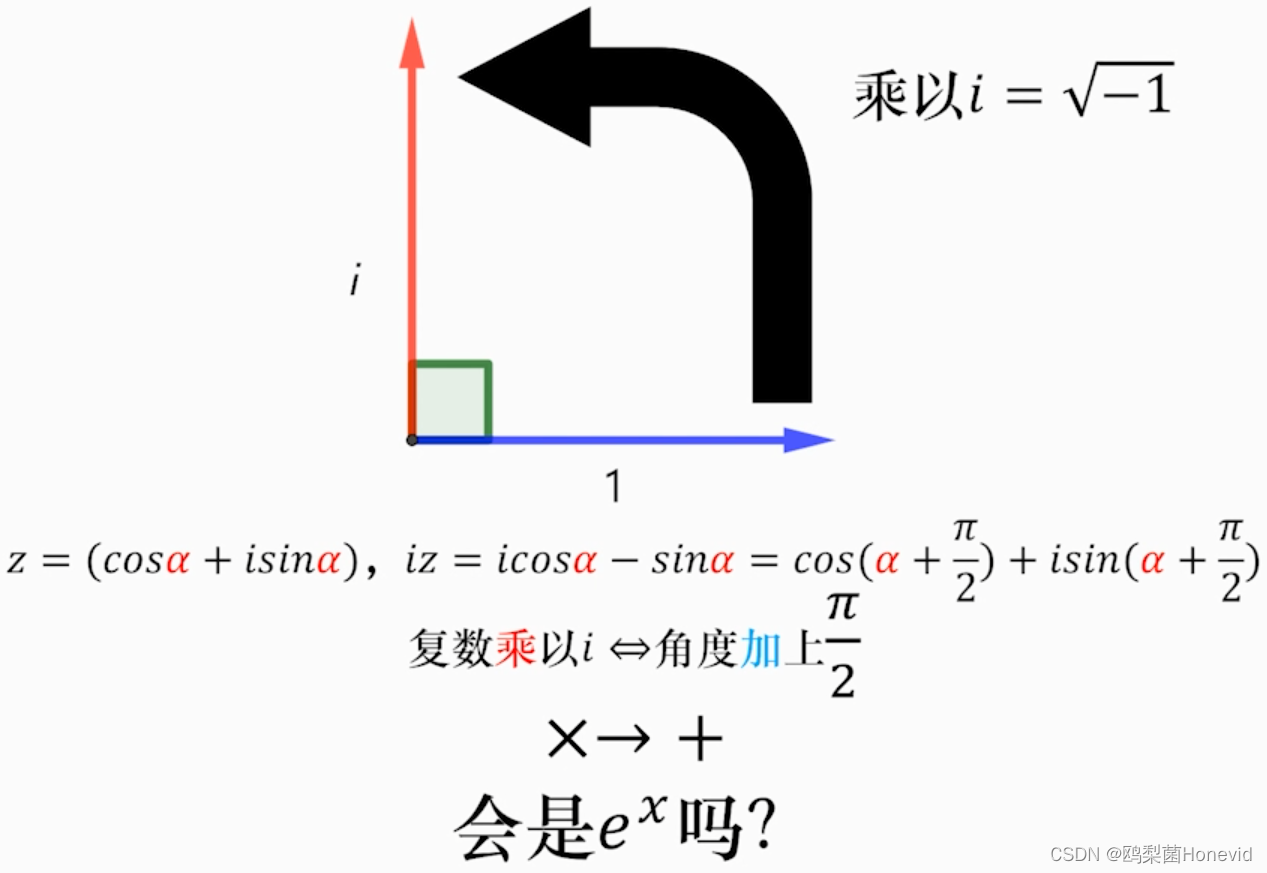
此处请联想到上述的同态映射,即: e x ∗ e y = e x + y e^x*e^y=e^{x+y} ex∗ey=ex+y,即 f ( x ) + f ( y ) = f ( x + y ) f(x)+f(y)=f(x+y) f(x)+f(y)=f(x+y),下面是通过python对猜想进行证实

作图
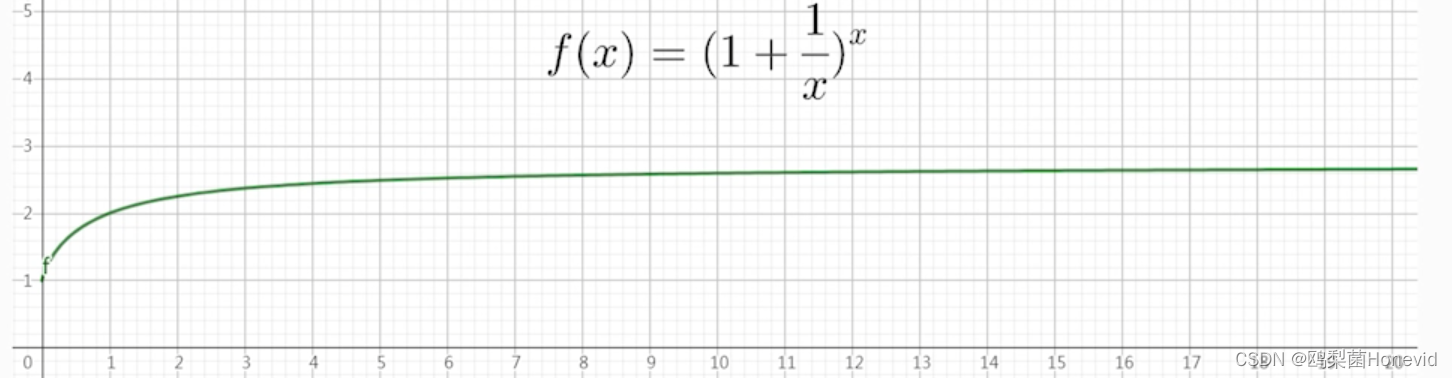
即:
lim n → ∞ ( 1 + 1 n ) n = e \begin{aligned}\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n&=e\end{aligned} n→∞lim(1+n1)n=e
lim n → ∞ ( 1 + a n ) n = [ lim n → ∞ ( 1 + a n ) n a ] a ⟶ t = n a [ lim t → ∞ ( 1 + 1 t ) t ] a = e a \lim_{n\to\infty}\left(1+\frac{\color{red}{a}}n\right)^n=\left[\lim_{n\to\infty}\left(1+\frac{\color{red}{a}}n\right)^{\color{red}{\frac{n}{a}}}\right]^a\overset{t=\frac na}{\operatorname*{\longrightarrow}}\left[\lim_{t\to\infty}\left(1+\frac1t\right)^t\right]^a=e^{\color{red}{a}} n→∞lim(1+na)n=[n→∞lim(1+na)an]a⟶t=an[t→∞lim(1+t1)t]a=ea
将a换成x,x也看作常数:
lim n → ∞ ( 1 + x n ) n = e x \lim_{n\to\infty}\left(1+\frac xn\right)^n=e^x n→∞lim(1+nx)n=ex
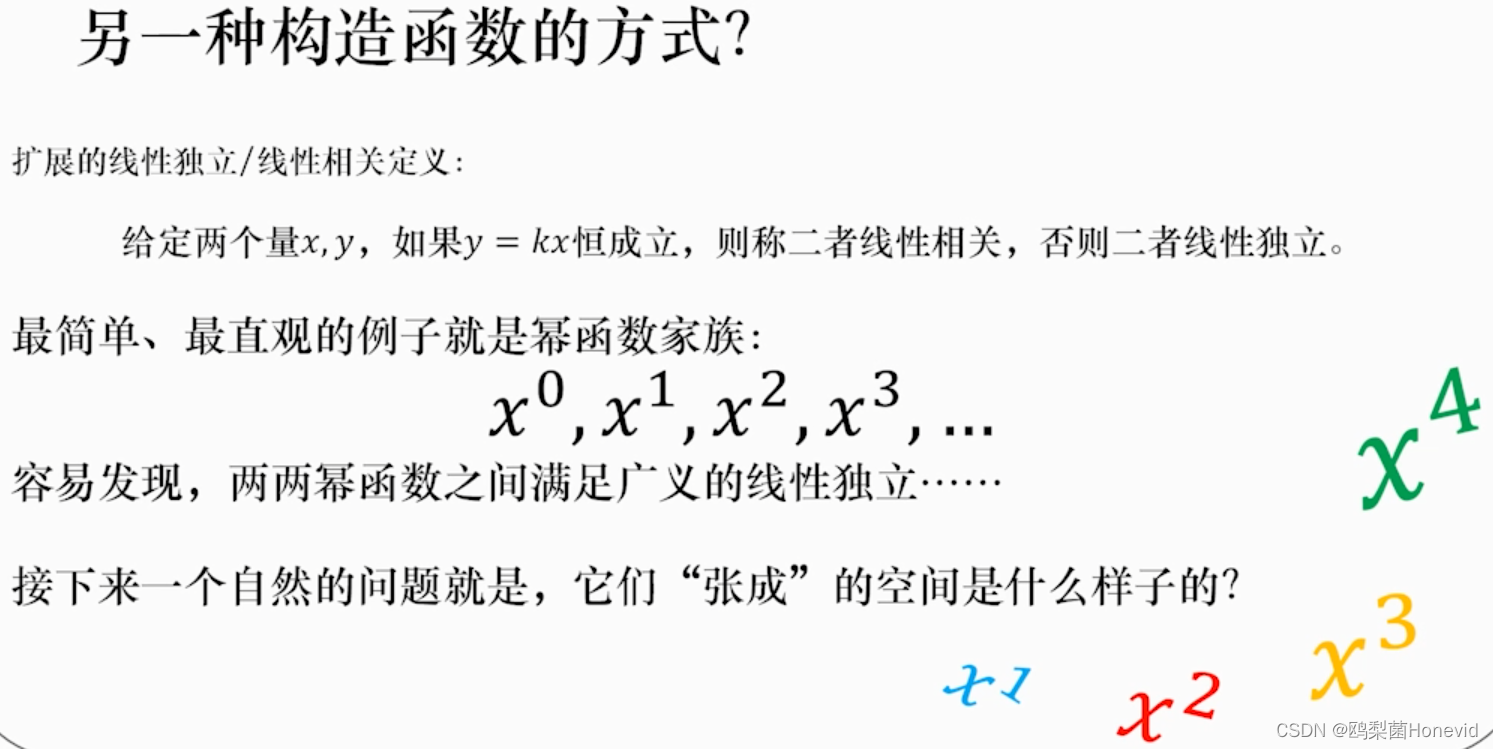
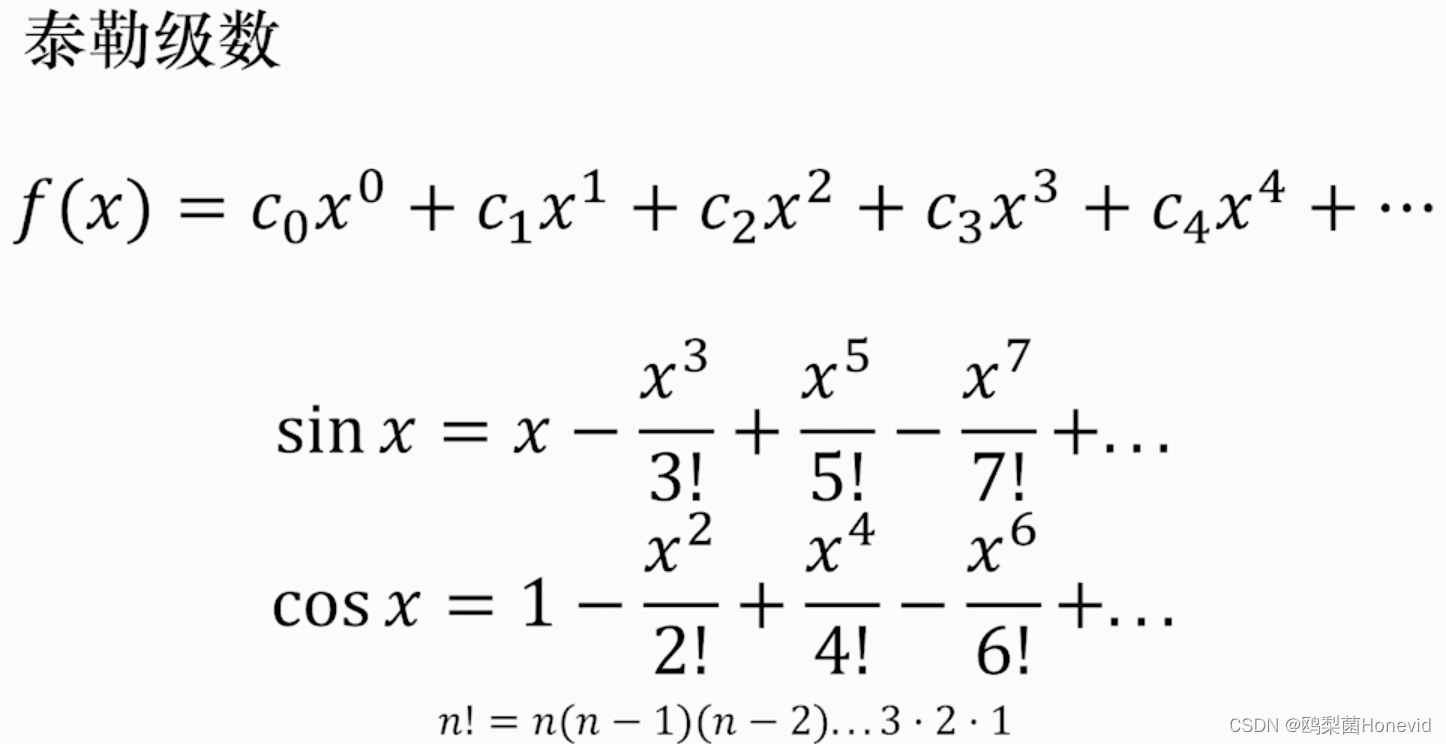
使用幂函数调整比例,从而张成新的函数
(看到这里我真的绷不住了,这个样子叫做零基础。。。还好我刚考过研,还记得些哈哈哈)
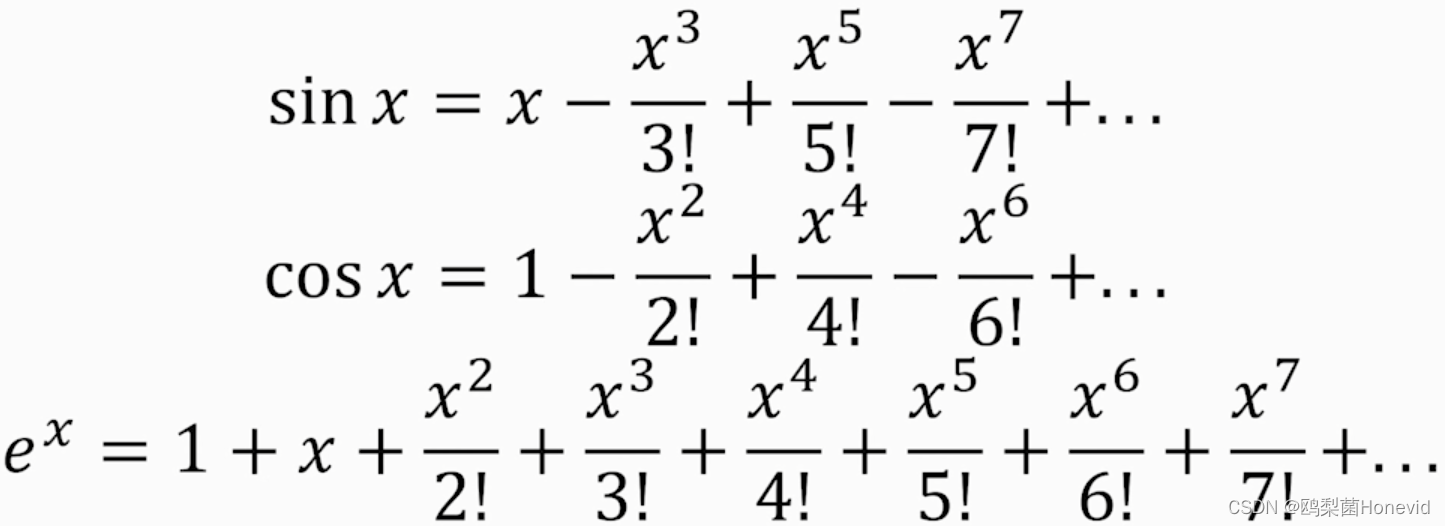
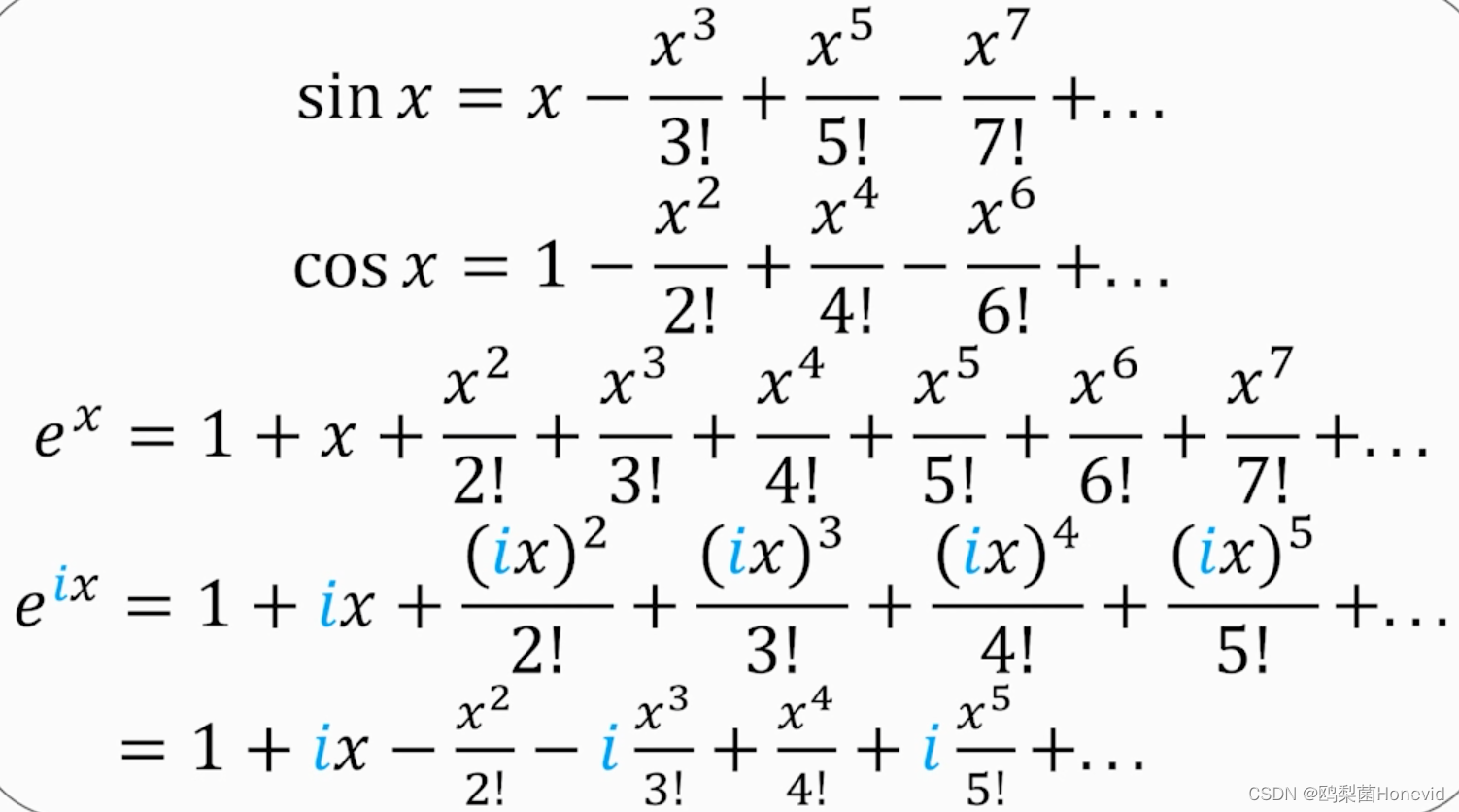
欧拉公式:
e i x = c o s x + i s i n x e^{ix}=cosx+isinx eix=cosx+isinx
从而有
z = r ( cos θ + i s i n θ ) = r e i θ z=r(\cos\theta+isin\theta)=re^{i\theta} z=r(cosθ+isinθ)=reiθ
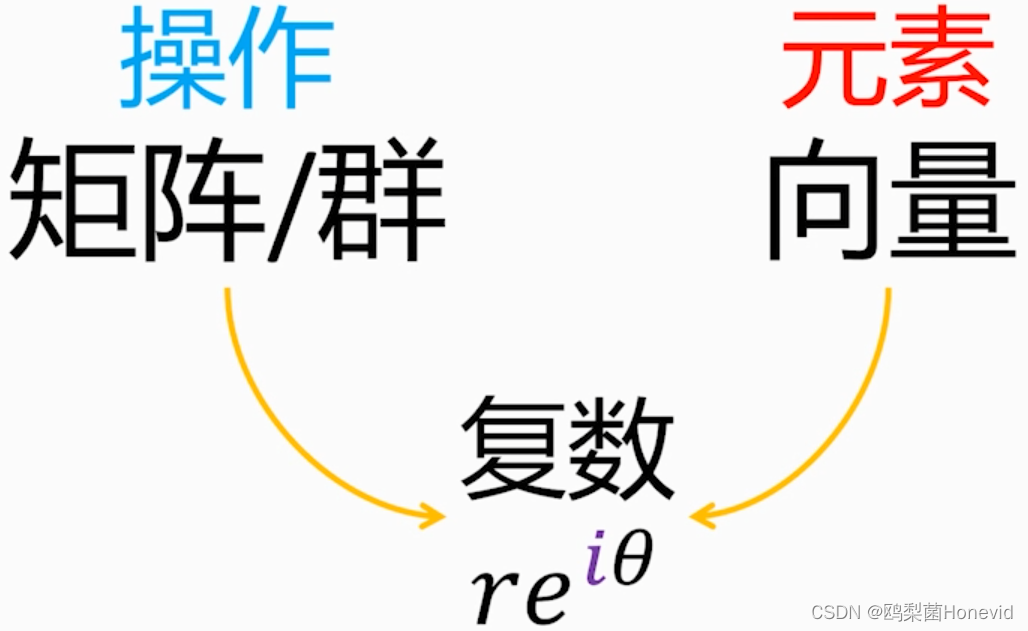


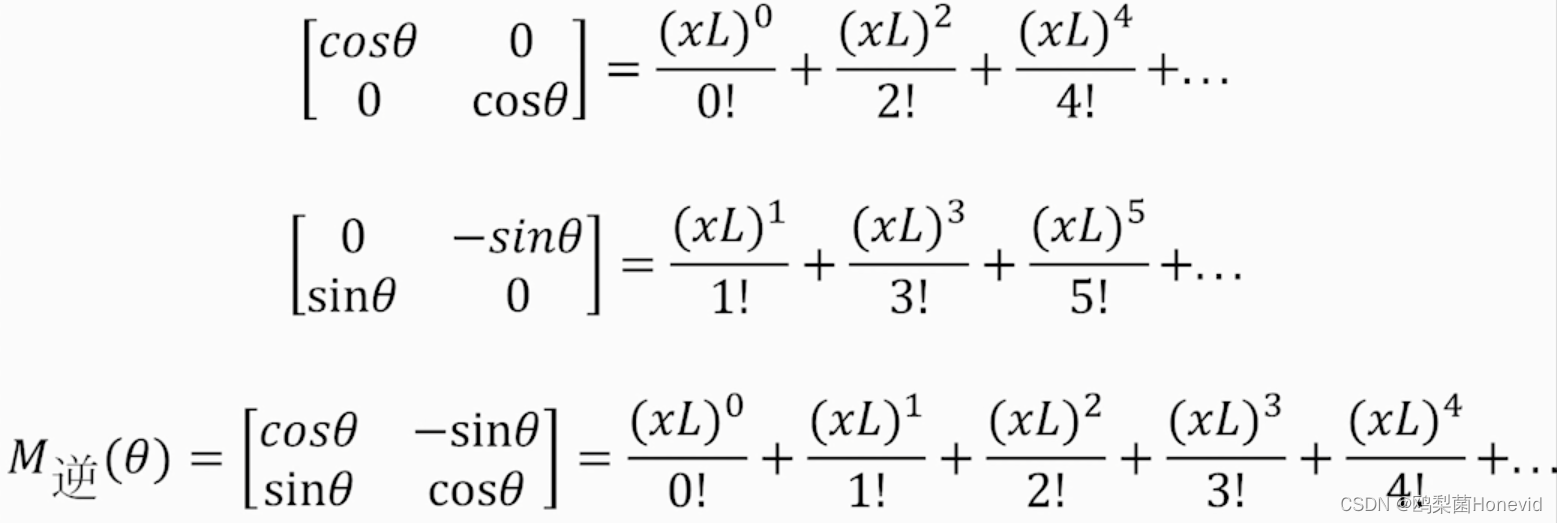
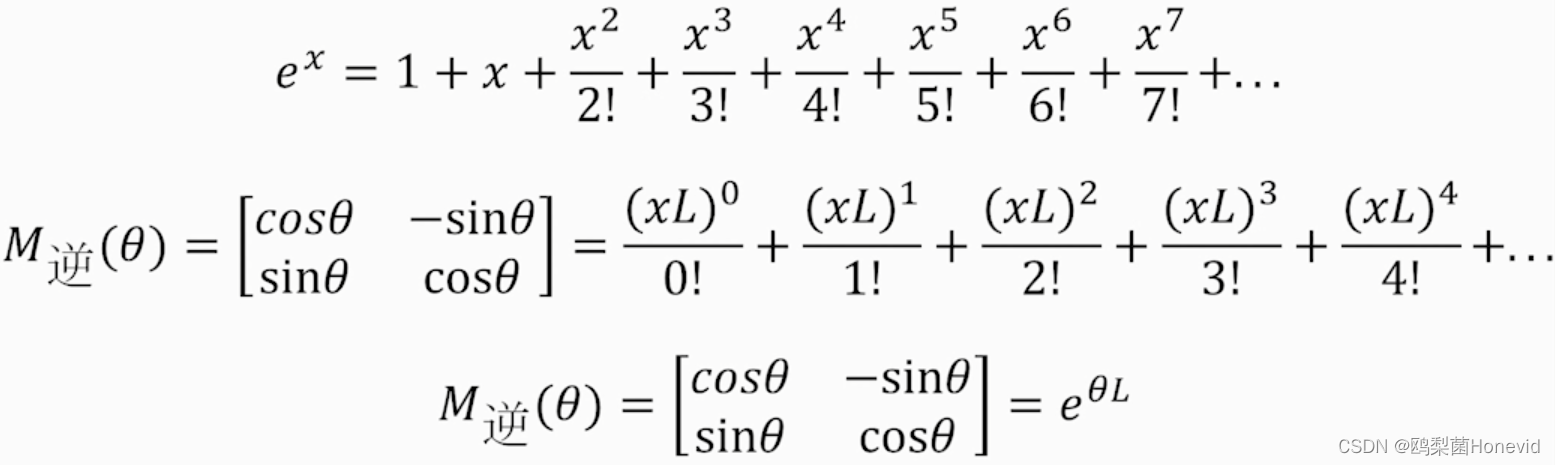
e L θ ν ⃗ ⇔ e^{L\theta}\vec{\nu}\Leftrightarrow eLθν⇔将 v ⃗ \vec{v} v逆时针转动角度 θ \theta θ
e i θ e^{i\theta} eiθ z ⇔ z\Leftrightarrow z⇔将 z z z逆时针转动角度 θ \theta θ

