深圳设计网站开发一份完整的活动策划方案

准备开始复习莫比乌斯反演，杜教筛这一部分，先复习一下数论分块

0.随便说说

数论分块可以计算如下形式的式子${\sum }_{i=1}^{n}f(i)g(\lfloor \frac{n}{i}\rfloor )$。
利用的原理是$\lfloor \frac{n}{i}\rfloor$的不同的值不超过$2\sqrt{n}$个。
当我们可以在$O(1)$的时间快速处理出${\sum }_{i=l}^{r}f(i)$或提前预处理出$f(x)$的前缀和时，上述式子可在$O(\sqrt{n})$的时间计算出来。

1.代码实现

怎么找每个块是个问题，有个结论：
设块的左端点为$\lfloor \frac{n}{l}\rfloor$，右端点为$\lfloor \frac{n}{r}\rfloor$，则$r=\lfloor \frac{n}{\lfloor \frac{n}{l}\rfloor }\rfloor$。

证明也挺好证的 设$k=\lfloor \frac{n}{i}\rfloor ,$则$k\le \frac{n}{i},$
因此$\lfloor \frac{n}{k}\rfloor \ge \lfloor \frac{n}{\frac{n}{i}}\rfloor =i$，即$i\le \lfloor \frac{n}{k}\rfloor =\lfloor \frac{n}{\lfloor \frac{n}{i}\rfloor }\rfloor$因此右端点$r=i_{max}=\lfloor \frac{n}{\lfloor \frac{n}{i}\rfloor }\rfloor$。

因此每个块为$i=l$到$i=\lfloor \frac{n}{\lfloor \frac{n}{i}\rfloor }\rfloor$。

2.例题

先顺手把$OIWiki$上的三个例题做了吧

UVA11526 H(n)

题面
用洛谷的题面了，这题就是求${\sum }_{i=1}^n\lfloor \frac{n}{i}\rfloor$，就是板子题，相当于$f(x)=1,g(n/i)=n/i$。注意如果$n=2147483647$，最后一次$nxt+1$会爆$int$，$UVA$神奇$oj$会报$RE$，所以就都开$longlong$就行，时间复杂度$O(T\sqrt{n})$。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int t,n;
int main(){cin>>t;while(t--){cin>>n;ll nxt=0,ans=0;for(ll i=1;i<=n;i=nxt+1){nxt=n/(n/i);ans+=(nxt-i+1)*(n/i);}cout<<ans<<endl;}
}

P2261 [CQOI2007] 余数求和

题面
Solution
$OI$时期的博客有这道题，题解挂链接了，随手一推就是这样，减号左边是$nk,$右侧用数论分块做

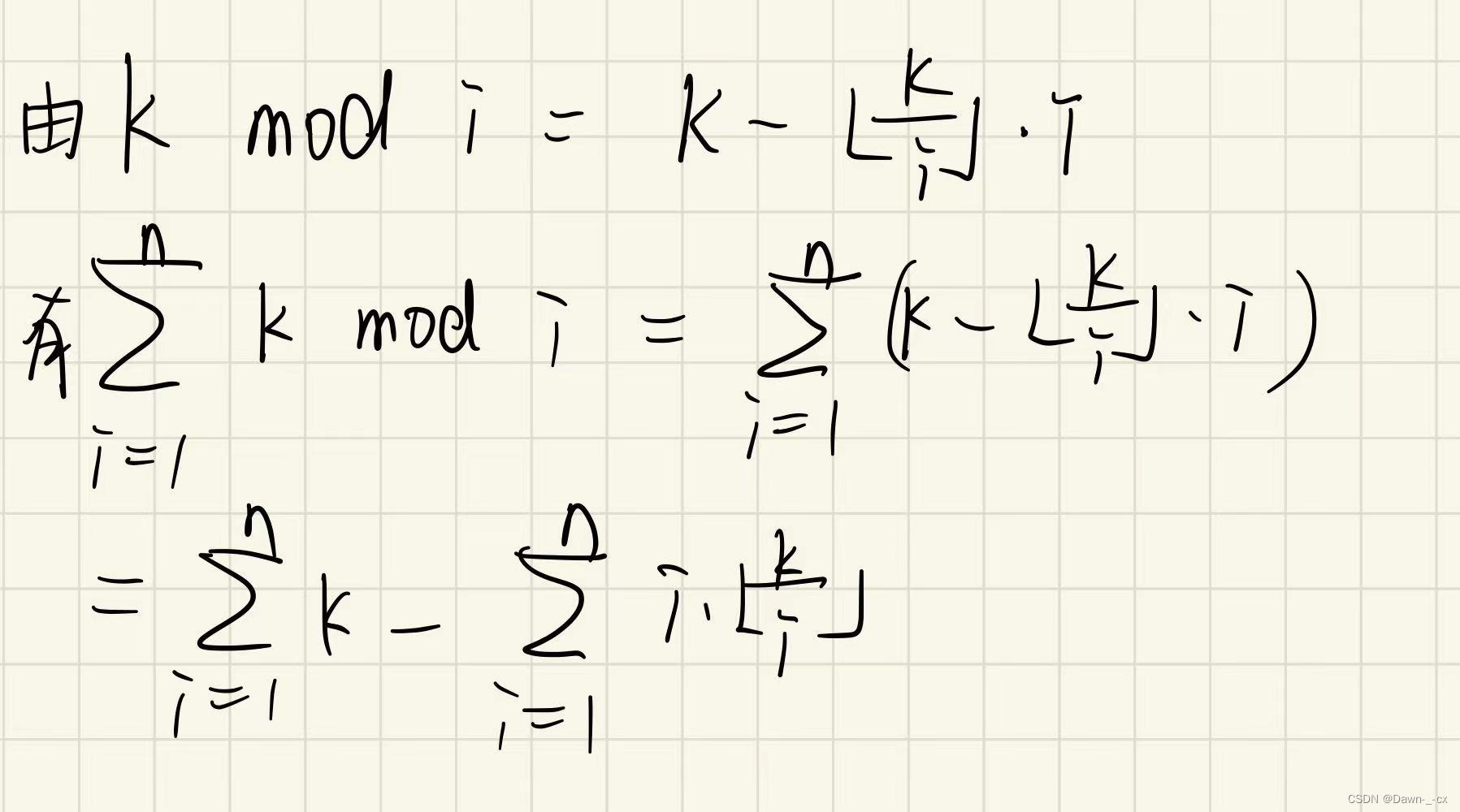
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,k,ans,nxt,sum;
inline ll s(ll n){return n*(n+1)/2;
}
int main(){cin>>n>>k;ans=n*k;for(int i=1;i<=min(n,k);i=nxt+1){nxt=min(k/(k/i),n);sum+=(s(nxt)-s(i-1))*(k/i);}cout<<ans-sum<<endl;
}

P3455 [POI2007] ZAP-Queries

题面

最后用个二维数论分块就可
闲得没事 这题想多打几个空格

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 5e4 + 100;
int cnt, pri[maxn], mu[maxn], s_mu[maxn];
bool vis[maxn];
inline void read(int &x) {int s = 0, w = 1; char ch = getchar();while (ch < '0' || ch > '9') {if(ch == '-') w = -1; ch = getchar(); }while (ch >= '0' && ch <= '9') {s = (s << 3) + (s << 1) + (ch & 15); ch = getchar(); }x = s * w;
}
void setup() {mu[1] = 1;for (int i = 2; i <= maxn - 100; i++) {if(!vis[i]) pri[++cnt] = i, mu[i] = -1;for (int j = 1; j <=cnt && i * pri[j] <= maxn - 100; j++) {vis[i * pri[j]] = true;if(i % pri[j]) mu[i * pri[j]] = -mu[i];else {mu[i * pri[j]] = 0;break;}}}for (int i = 1; i <= maxn - 100; i++) s_mu[i] = s_mu[i - 1] + mu[i];
}
int T, a, b, d, nxt;
int main() {setup();read(T);while(T--) {read(a), read(b), read(d);a /= d, b /= d;if(a > b) a ^= b, b ^= a, a ^= b;ll ans = 0;for (int i = 1; i <= a; i = nxt + 1) {nxt = min(a / (a / i), b / (b / i));ans += 1ll * (s_mu[nxt] - s_mu[i - 1]) * (a / i) * (b / i);}printf("%lld\n", ans);}
}

放两道套路题，这一类题都是以${\sum }_{i=1}^n{\sum }_{j=1}^{n}f(gcd(i,j))$形式的，我们要将$gcd(i,j)$提出来，作如下变化：

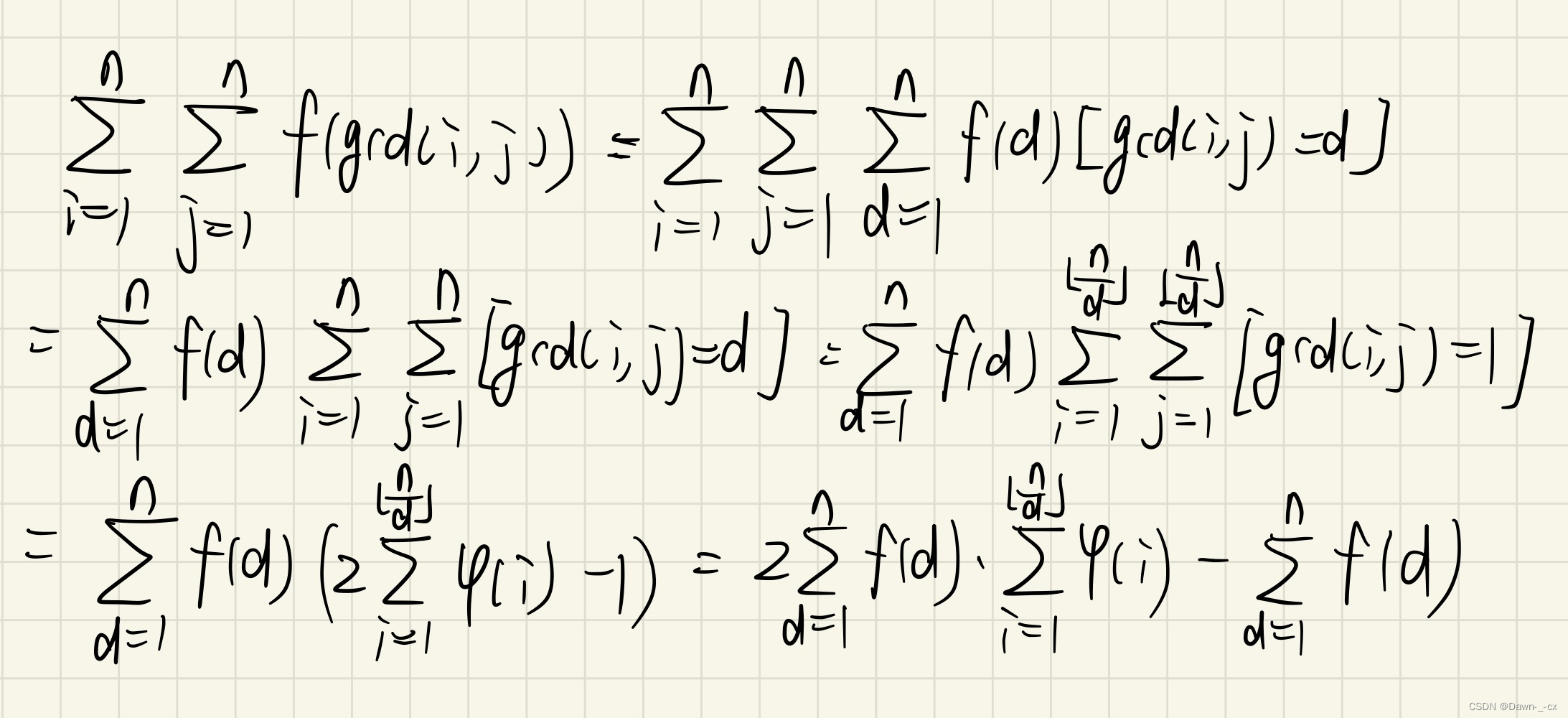
然后求出$f(x),\varphi (x)$的前缀和并应用数论分块解决。
后面两题的数据范围不一样，第一题是$n\le 1e7$，第二题是$n\le 1e9$，前者可以应用朴素的筛法求出欧拉函数前缀和，后者要用到杜教筛进行求解。

bzoj4804 欧拉心算

题面

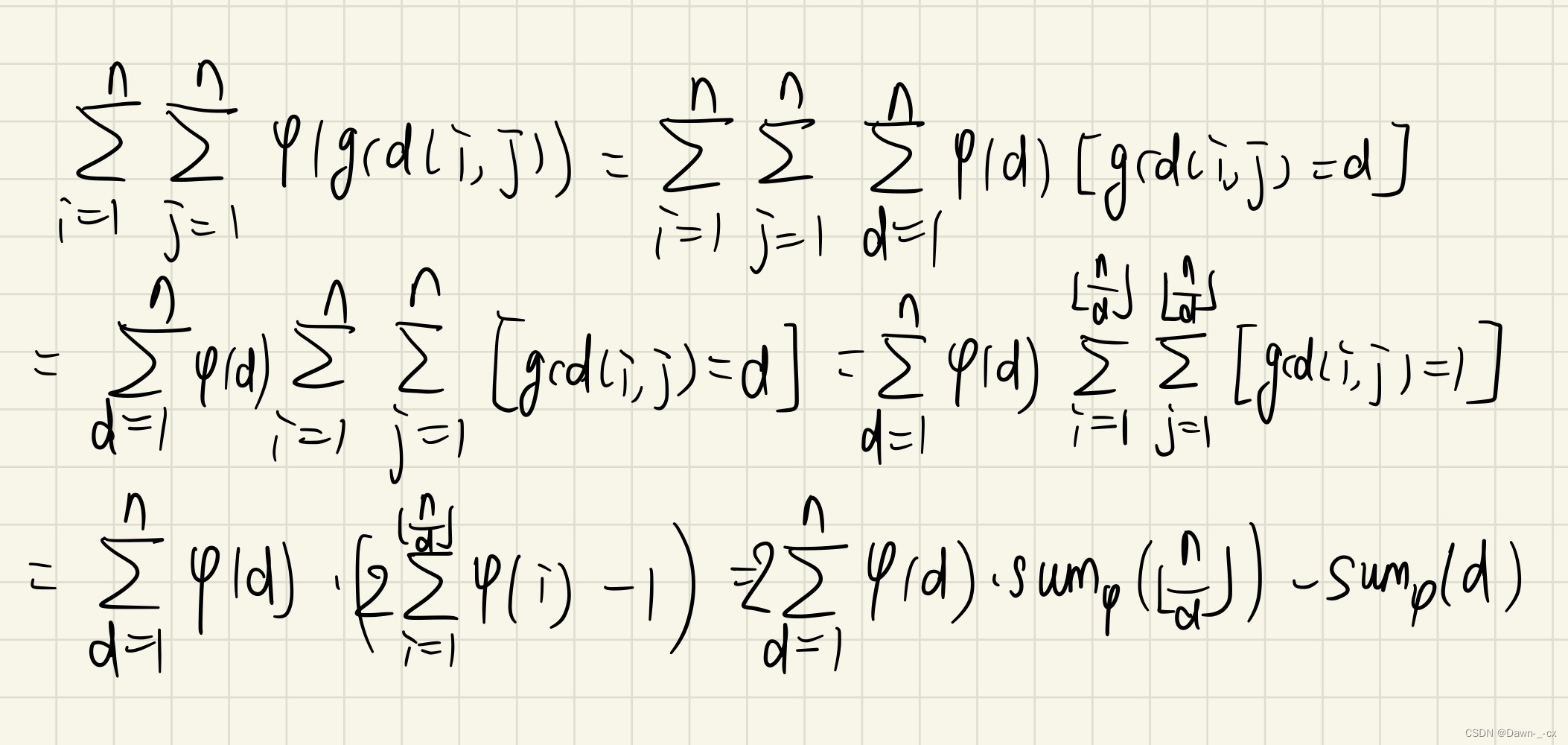
预处理出欧拉函数前缀和，应用数论分块即可。
写错了，最后是$sum\varphi (n)$。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn = 1e7 + 10;
int cnt, pri[maxn], euc[maxn];
ll s[maxn];
bool vis[maxn];
void setup(){euc[1] = 1;for (int i = 2; i <= maxn - 10; i++) {if (!vis[i]) pri[++cnt] = i, euc[i] = i - 1;for (int j = 1; j <= cnt && i * pri[j] <= maxn - 10; j++) {vis[i * pri[j]] = true;if (i % pri[j]) euc[i * pri[j]] = euc[i] * (pri[j] - 1);else {euc[i * pri[j]] = pri[j] * euc[i];break;}}}for (int i = 1; i <= maxn - 10; i++) s[i] = s[i - 1] + euc[i];
}
int T, n;
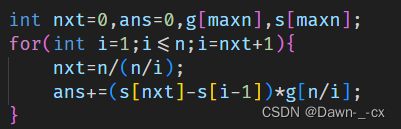
int main() {setup();scanf("%d", &T);while (T--) {scanf("%d", &n);int nxt = 0; ll ans = 0;for (int i = 1; i <= n; i = nxt + 1) {nxt = n / (n / i);ans += (s[nxt] - s[i - 1]) * s[n / i];}printf("%lld\n", 2ll * ans - s[n]);}
}

HDU7325 GCD Magic

题面
考场上考到得，打了$150$行，$MLE$了一次，$WA$了一次，最后过了
$MLE$是因为对$sbHDUOJ$不信任，预处理的$1e7$的欧拉函数前缀和，后来改成了$2e6$，$WA$了，看了一会儿发现是因为杜教筛欧拉函数前缀和没模$mod$导致后面计算答案时候爆$longlong$了，改过来交一发对了，太不容易了，这要再错真不知道要$debug$到哪年去。
思路如下，就不打公式了，太多了，手写了。

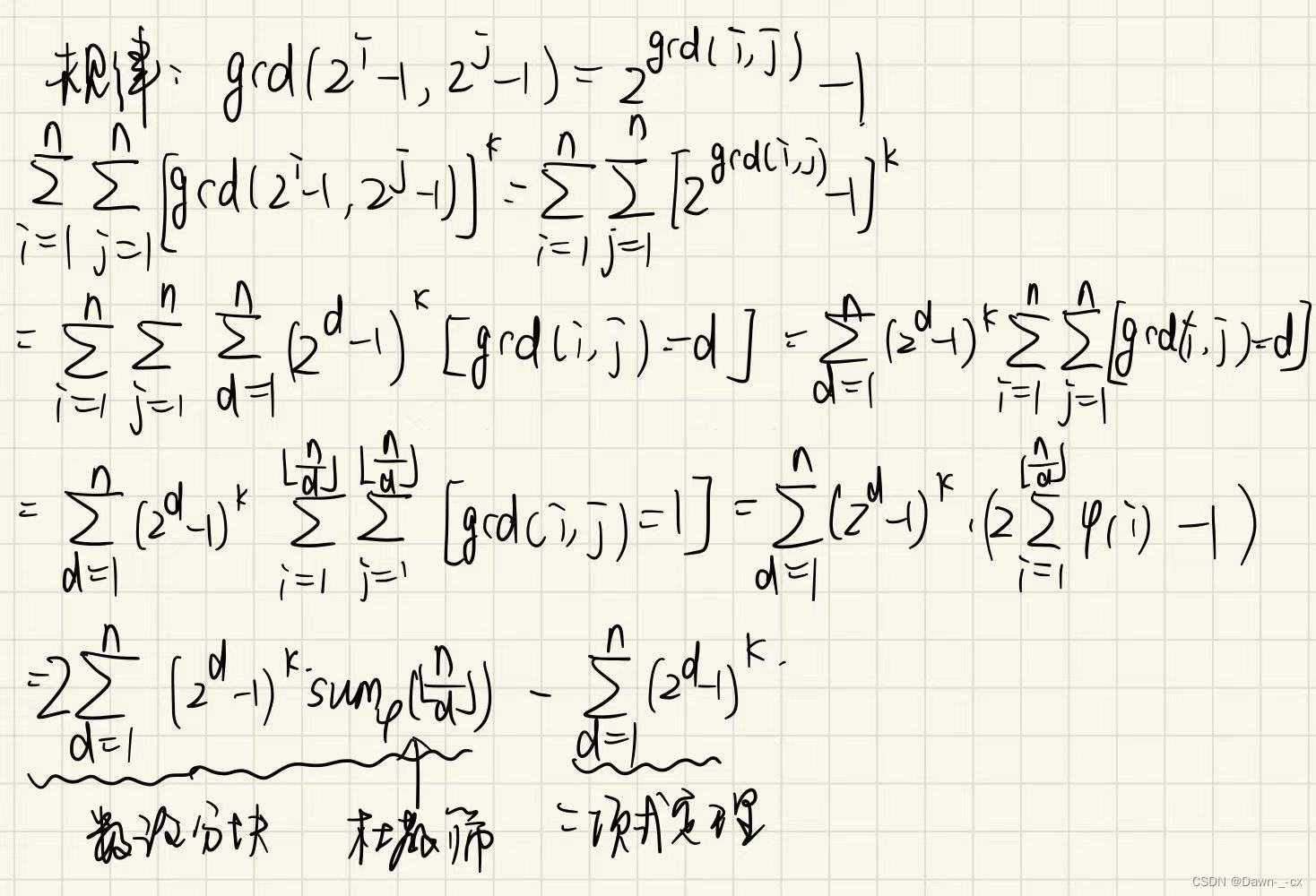
上代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
const int maxn = 2000010;
inline void read(int &x)
{int s = 0, w = 1;char ch = getchar();while (ch < '0' || ch > '9'){if (ch == '-')w = -1;ch = getchar();}while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch & 15);ch = getchar();}x = s * w;
}
ll ans, s[maxn], frac[20], fracinv[20];
int t, n, k, lst;
ll pri[maxn], euc[maxn], cur, mu[maxn], sum_mu[maxn];
bool vis[maxn];
map<ll, ll> mp_mu;ll S_mu(ll x)
{if (x < maxn)return sum_mu[x];if (mp_mu[x])return mp_mu[x];ll ret = (ll)1;for (ll i = 2, j; i <= x; i = j + 1){j = x / (x / i);ret -= S_mu(x / i) * (j - i + 1);}return mp_mu[x] = ret % mod;
}ll S_phi(ll x)
{ll ret = (ll)0;ll j;for (ll i = 1; i <= x; i = j + 1){j = x / (x / i);ret += (S_mu(j) - S_mu(i - 1)) * (x / i) * (x / i);}return ((ret - 1) / 2 + 1) % mod;
}
inline ll qpow(ll x, ll y)
{ll re = 1LL;while (y){if (y & 1)(re *= x) %= mod;(x *= x) %= mod;y >>= 1;}return re;
}
inline ll inv(ll x)
{return qpow(x, mod - 2);
}
void setup()
{frac[0] = fracinv[0] = 1LL;for (int i = 1; i <= 15; i++)frac[i] = 1ll * frac[i - 1] * i % mod;fracinv[15] = inv(frac[15]);for (int i = 14; i; i--)fracinv[i] = 1ll * fracinv[i + 1] * (i + 1) % mod;euc[1] = 1;mu[1] = 1;for (int i = 2; i < maxn; i++){if (!vis[i]){pri[++cur] = i;mu[i] = -1;euc[i] = i - 1;}for (int j = 1; j <= cur && i * pri[j] < maxn; j++){vis[i * pri[j]] = true;if (i % pri[j])mu[i * pri[j]] = -mu[i], euc[i * pri[j]] = euc[i] * euc[pri[j]];else{mu[i * pri[j]] = 0;euc[i * pri[j]] = euc[i] * pri[j];break;}}}for (int i = 1; i < maxn; i++)s[i] = (1ll * s[i - 1] + euc[i]) % mod;for (int i = 1; i < maxn; i++)sum_mu[i] = (1ll * sum_mu[i - 1] + mu[i]) % mod;
}
inline ll C(ll n, ll m)
{if (n < m)return 0;return 1ll * frac[n] * fracinv[m] % mod * fracinv[n - m] % mod;
}
inline ll seq(ll n, ll k)
{if (k == 0)return n;ll a1 = (1LL << k) % mod, q = (1LL << k) % mod;return 1LL * a1 * ((qpow(q, n) - 1 + mod) % mod) % mod * inv((q - 1 + mod) % mod) % mod;
}
inline ll sg(ll n, ll k)
{if (n == 0)return 0LL;ll ans = 0, flag = 1;for (int i = 0; i <= k; i++){ans = (1ll * ans + 1ll * ((flag + mod) % mod) * C(k, i) % mod * seq(n, k - i) % mod) % mod;flag *= (-1ll);}return ans % mod;
}
int main()
{setup();read(t);while (t--){read(n), read(k);ans = 0ll;lst = 0;for (int i = 1; i <= n; i = lst + 1){lst = n / (n / i);ll snow = 0;if (n / i >= maxn - 10)snow = S_phi(n / i);elsesnow = s[n / i];ans = (1ll * ans + (1ll * sg(lst, k) - sg(i - 1, k) + mod) % mod * snow % mod) % mod;}printf("%lld\n", (2LL * ans % mod - sg(n, k) + mod) % mod);}
}