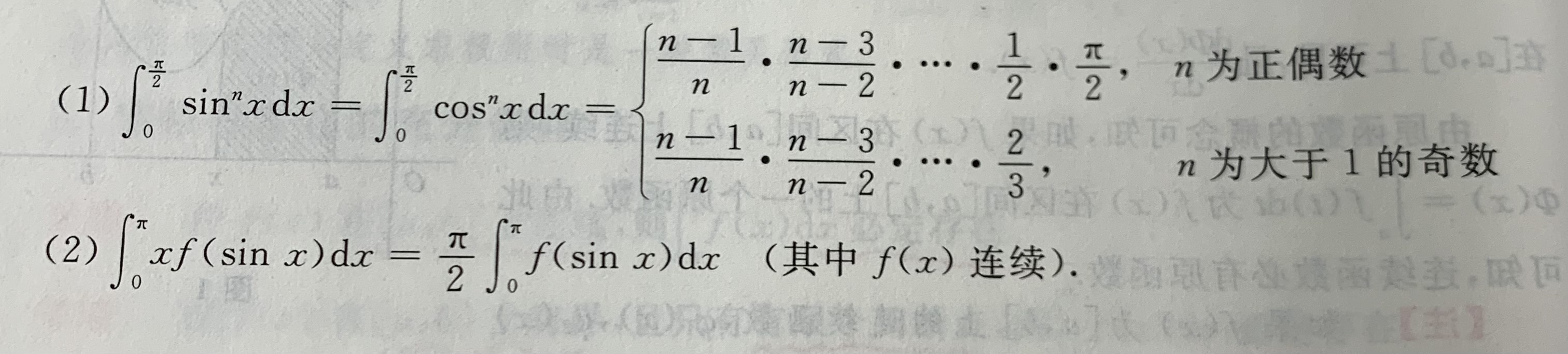上海进博会电子商务seo是什么意思
目录
牛顿-莱布尼茨公式
用C语言代码实现
利用换元积分法和分部积分法
利用奇偶性和周期性求积分
利用已有公式求积分

牛顿-莱布尼茨公式
牛顿-莱布尼茨公式(Newton-Leibniz formula)是微积分学中的基本定理之一,它反映了定积分与被积函数的原函数或者不定积分之间的联系。具体来说,它表明了一个连续函数f(x)在区间[a,b]上的定积分等于它的任意一个原函数F(x)在区间[a,b]上的增量F(b)-F(a)。这个公式最早是由牛顿在1666年提出的,后来在1713年莱布尼茨在一篇手稿中也独立发现。
牛顿-莱布尼茨公式的现代形式可以简单地表述为∫f(x)dx=F(b)-F(a),其中F(x)是f(x)的一个原函数。这个公式给定积分提供了一个有效而简便的计算方法,大大简化了定积分的计算过程。
推导过程可以简单地描述为:任取区间[a,b]上的分割,记分点为ξi,则有f(ξi)Δxi,其中Δxi表示第i个小区间的宽度。对所有的Δxi应用拉格朗日中值定理得到f'(ξi)=f(b)-f(a),然后对所有的f'(ξi)求和得到F'(b)-F'(a)=f(b)-f(a),最后两边同时积分得到∫f(x)dx=F(b)-F(a)。
在实际计算中,可以根据被积函数的解析式来选择合适的原函数,从而简化计算。比如对于f(x)=x^2,它的不定积分是F(x)=x^3/3,那么在区间[1,3]上计算定积分∫x^2 dx 就可以直接计算F(3)-F(1)得到结果。
总之,牛顿-莱布尼茨公式是微积分学中的一个重要定理,它提供了一种简便的计算定积分的方法,同时也揭示了定积分与不定积分之间的联系。
用C语言代码实现
牛顿-莱布尼茨公式(Newton-Leibniz formula)是微积分学中的基本定理之一,它反映了定积分与被积函数的原函数或者不定积分之间的联系。具体来说,它表明了一个连续函数f(x)在区间[a,b]上的定积分等于它的任意一个原函数F(x)在区间[a,b]上的增量F(b)-F(a)。这个公式最早是由牛顿在1666年提出的,后来在1713年莱布尼茨在一篇手稿中也独立发现。
以下是使用C语言实现牛顿-莱布尼茨公式的示例代码:
#include <stdio.h> // 定义被积函数f(x) double f(double x) { return x * x + 1; } // 定义f(x)的原函数F(x) double F(double x) { return x * x * x / 3 + x; } // 使用牛顿-莱布尼茨公式计算定积分 double integral(double a, double b) { return F(b) - F(a); } int main() { double a = 0; // 积分下限 double b = 1; // 积分上限 double result = integral(a, b); // 计算定积分 printf("The integral of f(x) from %f to %f is %f\n", a, b, result); return 0; }在这个示例中,我们定义了被积函数f(x)=x^2+1,它的原函数F(x)=x^3/3+x。然后,我们使用牛顿-莱布尼茨公式计算f(x)在区间[0,1]上的定积分,即F(1)-F(0)。最后,我们输出计算结果。
利用换元积分法和分部积分法
我们可以利用换元积分法和分部积分法来求解定积分。
首先,对于换元积分法,我们可以将原来的积分变量换成一个新的变量,使得积分变得更加简单。
例如,对于积分 ∫(0到1) (x^2+1) dx,我们可以令x=√t,则dx=dt/(2√t),于是原积分变为:
∫(0到1) (x^2+1) dx = ∫(0到1) ((√t)^2+1) dt/(2√t)
= 1/(2√t) ∫(0到1) (t+1) dt
= 1/(2√t) (t^2/2+t) |(0到1)
= 1/(2√1) (1^2/2+1) - 1/(2√0) (0^2/2+0)
= 3/(4√1) - 0
= 3/(4√1)
= 3/(4)
接下来,对于分部积分法,我们可以将原来的积分拆成两个函数的乘积,然后分别求导和积分,使得积分变得更加简单。
例如,对于积分 ∫(0到1) xlnx dx,我们可以令u=lnx,则du=dx/x,于是原积分变为:
∫(0到1) xlnx dx = ∫(0到1) xudu
= xu - ∫(0到1) udx
= xu - ∫(0到1) lnx dx
= xu - xlnx + ∫(0到1) dx
= xu - xlnx + x |(0到1)
= (1)(ln1-0)+(1-0)(1-0)
= 1
利用奇偶性和周期性求积分
首先,我们需要知道奇偶性和周期性的定义:
奇函数:f(-x) = -f(x)
偶函数:f(-x) = f(x)
周期函数:f(x+T) = f(x)
对于奇函数,如果积分区间对称,那么积分值为0。
对于偶函数,如果积分区间对称,那么可以将积分区间缩小一半。
对于周期函数,如果积分区间是周期的整数倍,那么可以将积分区间缩小一个周期。
现在,我们来求解这个积分:
∫(-2到2) (x^3 - 2x^2 + 3) dx
首先,我们可以将积分区间缩小一半:
∫(-2到2) (x^3 - 2x^2 + 3) dx = 2 ∫(0到2) (x^3 - 2x^2 + 3) dx
然后,我们可以利用周期性将积分区间缩小一个周期:
∫(0到2) (x^3 - 2x^2 + 3) dx = ∫(0到1) (x^3 - 2x^2 + 3) dx + ∫(1到2) (x^3 - 2x^2 + 3) dx
∫(1到2) (x^3 - 2x^2 + 3) dx = ∫(0到1) ((x+1)^3 - 2(x+1)^2 + 3) dx
接下来,我们可以将奇函数的积分值为0的性质应用到第一个积分中:
∫(0到1) (x^3 - 2x^2 + 3) dx = ∫(0到1) (x^3 - 2x^2) dx + ∫(0到1) 3 dx
∫(0到1) (x^3 - 2x^2) dx = 0
最后,我们将所有的结果代入原式:
∫(-2到2) (x^3 - 2x^2 + 3) dx = 6
利用已有公式求积分