h5网站制作报价推广平台收费标准

1 矩阵的特征值和特征向量究竟是什么？

矩阵实际上是一种变换,是一种旋转伸缩变换（方阵） 不是方阵的话还有可能是一种升维和降维的变换
直观理解可以看系列超赞视频线性代数-哔哩哔哩_Bilibili

比如A=$\left(\begin{array}{cc}1& 2\\ 2& 1\end{array}\right)$ x=$\left(\begin{array}{c}1\\ 2\end{array}\right)$

我们给x左乘A实际上是对x进行了一次旋转伸缩变换 Ax=$\left(\begin{array}{c}5\\ 4\end{array}\right)$

而我们如果仅仅是单纯的伸缩变换，而如果A对x仅仅只能伸缩变换，而不能旋转变换，则称为x为矩阵A的特征向量，伸缩变换的倍数即为特征值

2 求特征值和特征向量

（1）写出特征多项式$|E-A|=0$ 求得特征值

（2）代入特征值求解方程组，解即为我们的特征向量

矩阵的迹

矩阵乘积为行列式

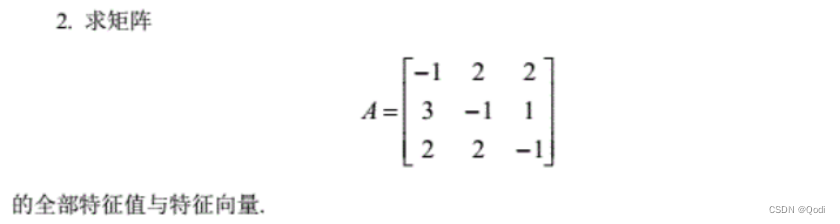
3 特征值和特征向量的应用

已知A的特征值

则$A^{-1}$的特征值可求

A的一个多项式特征值可求

所以把我们要求的值转换为A的多项式，进而求出特征值，求出行列式的值

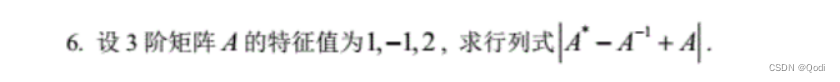
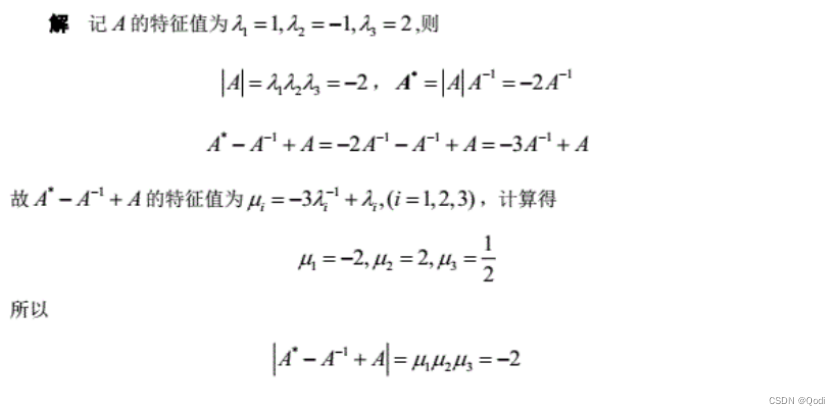
4 矩阵的对角化

非对称矩阵对角化

（1）求解特征值和特征向量

（2）特征向量组成我们的相乘矩阵P 特征值作为主对角线上的元素的对角矩阵就是我们对角化的矩阵

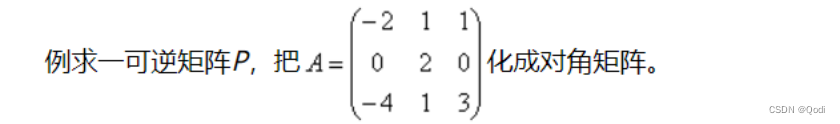
对称矩阵对角化求正交矩阵

（1）求解特征值值和特征向量

（2）施密特正交化重根对应的特征向量，再单位化所有特征向量

（3）取向量依次组成我们的正交矩阵Q