同ip网站过多是空间的原因还是域名的原因品牌推广渠道
目录
堆
堆的概念
堆的性质
堆的创建
1、堆向下调整
2、堆的创建
3、建堆的时间复杂度
堆的插入和删除
1、堆的插入
2、堆的删除
堆的应用
1、优先级队列的实现
2、堆排序
3、Top-k问题
堆 （Heap）
堆的概念
前面介绍的优先级队列在JDK1.8中其底层使用了堆的数据结构，而堆实际就是在完全二叉树的基础之上进行了一些元素的调整。
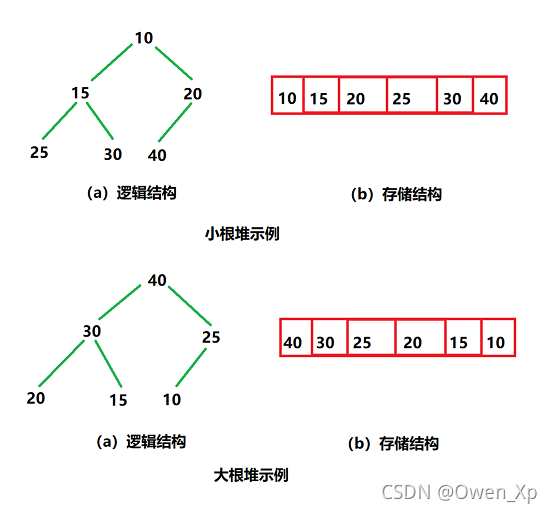
如果有一个 关键码的集合 K = {k0 ， k1 ， k2 ， … ， kn-1} ，把它的所有元素 按完全二叉树的顺序存储方式存储 在一 个一维数组中 ，并满足： Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >=K2i+2) i = 0 ， 1 ， 2… ，则 称为小堆 ( 或大堆) 。（即双亲比孩子的数值小(大)——小(大)堆）将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
堆的性质
- 堆中某个节点的值总是不大于或不小于其父节点的值；
- 堆总是一棵完全二叉树。
下面来看一下堆的可视化操作堆的可视化操作
https://visualgo.net/zh/heap
堆的创建
1、堆向下调整
对于集合 { 27,15,19,18,28,34,65,49,25,37 } 中的数据，如果将其创建成堆呢？
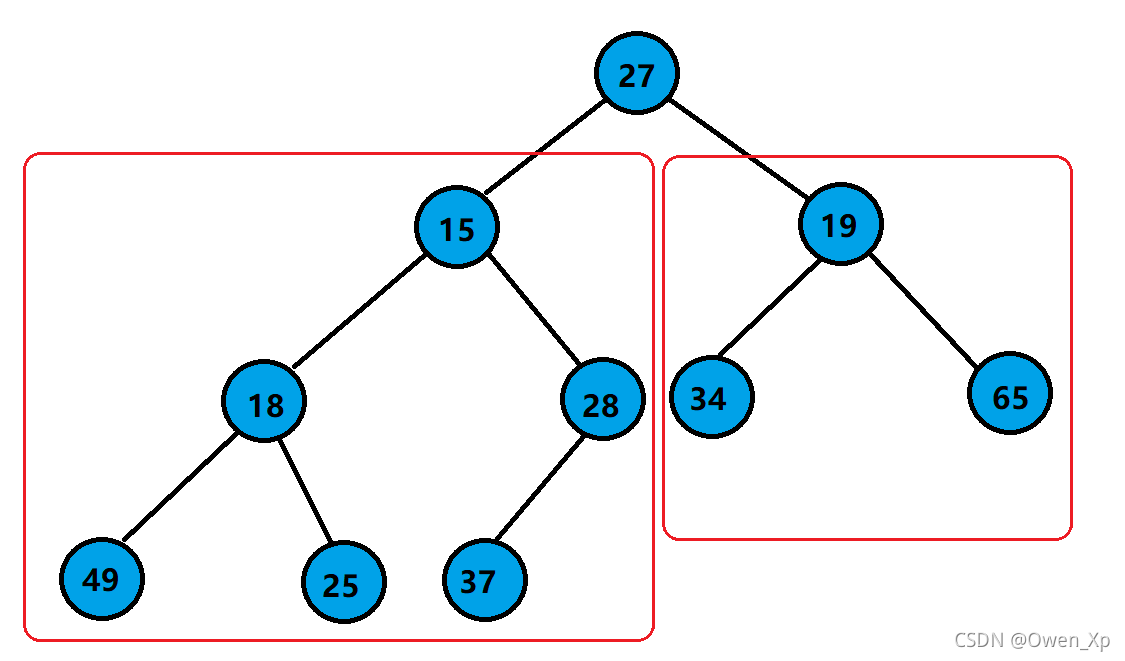
仔细观察上图后发现： 根节点的左右子树已经完全满足堆的性质，因此只需将根节点向下调整好即可 。
向下过程 ( 以小堆为例 ) ：
1. 让 parent 标记需要调整的节点， child 标记 parent 的左孩子 ( 注意： parent 如果有孩子一定先是有左孩子 )
2. 如果 parent<