当前位置：首页 > news >正文

网站后台什么语武汉新闻最新消息

news 2025/7/27 18:58:39

网站后台什么语,武汉新闻最新消息,宁乡小程序开发,上海推牛网络科技有限公司递归的定义大名鼎鼎的递归，相信你即使没接触过也或多或少听过，例如汉诺塔问题就是运用了递归的思想，对于一些学过c语言的同学来说，它可能就是噩梦，因为我当时就是这么认为的（不接受反驳doge） …

递归的定义

大名鼎鼎的递归，相信你即使没接触过也或多或少听过，例如汉诺塔问题就是运用了递归的思想，对于一些学过c语言的同学来说，它可能就是噩梦，因为我当时就是这么认为的（不接受反驳doge）

递归到底是什么捏，递归是一种解决问题的思想它将复杂的问题转换为无数嵌套的小规模同逻辑问题，可以简化代码，使问题易于理解,要理解递归一定要先理解递归函数

递归函数

一个直接或间接调用自己的函数，就是递归函数

递归函数一定包括递归条件和基线条件，递归条件就是调用自己的条件，基线条件则是结束递归的条件

⭐太抽象了，直接通过代码理解把

递归实现阶乘

public class recurrence {public static void main(String[] args) {//递归函数调用 factorial(4);//执行步骤://递归中的  递// 1.  求factorial(4)// return 4 * factorial(3)           由于factorial(3)未知，故该问题需先求解factorial（3）// 2.  求factorial(3)// return 3 * factorial(2)           同上由于factorial(2)未知，问题又转换为求factorial(2)// 3.  求factorial(2)// return 2 * factorial(1)           同上由于factorial(1)未知，问题又转换为求factorial(1)// 4.  求factorial(1)       // factorial(1)满足n = 1（满足基线条件，递归的 递 结束，开始进行 归 ） ,故factorial(1) = 1// 5.  由于factorial(1)=1得解，故factorial(2)继续执行，return 2，即factorial(2)=2// 6.  factorial(2)=2，故factorial(3)=6可解// 7.  factorial(3)=6，故factorial(4)=24可解// 8.  递归的 归 结束，函数结束}public static int factorial(int n){//基线条件if(n==1){return 1;}else{                  //递归条件return n*factorial(n-1); }}
}

细品应该不难理解，知识输入完毕，开始输出知识，下面进入递归的应用吧

数组的正反遍历

public static void ergodic(int[] arr ,int index){//正向遍历     由递遍历System.out.println(arr[index]);//递归                                                                                          if(index < arr.length-1 && 0 <= index) {       //递归条件ergodic(arr , index+1);}//反向遍历      由归遍历System.out.println(arr[index]);}

使用

ergodic(new int[]{1,2,3,4,5},0);

结果

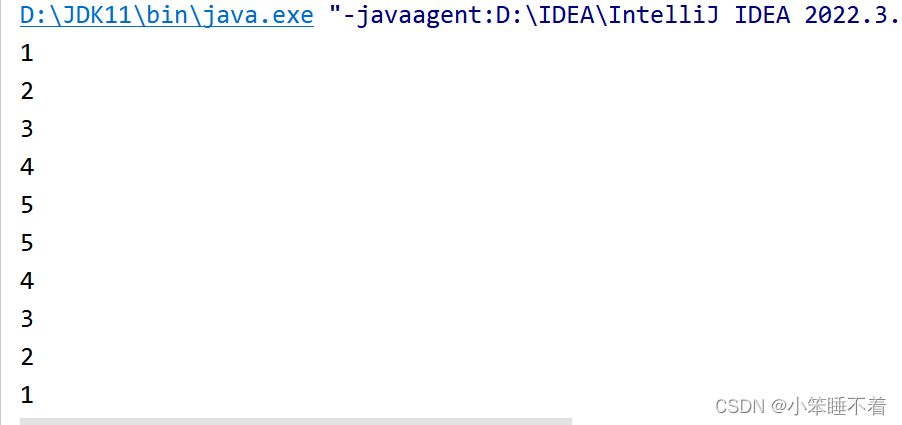
二分查找

不熟悉二分查找的可以看详解二分查找(Java)

public static int binarySearch(int[] arr, int target ,int l ,int r){if(l > r){return -1;}int mid=(l + r)>>>1;             //右移运算效果为 /2if(arr[mid]<target){return binarySearch(arr,target,mid+1,r);}else if(target < arr[mid]){return binarySearch(arr,target,l,mid-1);}else{return mid;}
}

冒泡排序（优化版）

public static void bubbloSort(int[] arr , int arrSize){int greatLeft=arrSize-1;for (int i = 0; i < arrSize-1; i++) {if(arr[i] > arr[i+1]){int temp;temp=arr[i];arr[i]=arr[i+1];arr[i+1]=temp;greatLeft=i;        //最后置换的位置可视为未排序的尾结点，因为后面没有置换说明后面是有序的不需要再冒泡了}}if(greatLeft!=arrSize-1){bubbloSort(arr , arrSize);}
}

插入排序

public static void insertSort(int[] arr ,int low){if(low==arr.length){return ;}for (int i = low; 0 < i; i--) {if(arr[i-1]>arr[i]){int temp=arr[i];arr[i]=arr[i-1];arr[i-1]=temp;}else {break;}}insertSort(arr,low+1);
}

多路递归

实现斐波那契数列

    //斐波那契数列public static int fibonacci(int n){if(n == 0){return 0;}else if(n == 1){return 1;}return fibonacci(n-1)+fibonacci(n-2);}

优化斐波那契

//(优化记忆）斐波那契数列public static int fibonacci(int n ){int[] arr =new int[n+1];Arrays.fill(arr,-1);arr[0]=0;arr[1]=1;return f(n ,arr);}private static int f(int n , int[] arr){if(arr[n]!=-1){return arr[n];}int value=f(n-1,arr)+f(n-2,arr);arr[n]=value;return value;}