今天最新的新闻头条排名seo怎么样

⭐️ 本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。

学习数据结构与算法的关键在于掌握问题背后的算法思维框架，你的思考越抽象，它能覆盖的问题域就越广，理解难度也更复杂。在这个专栏里，小彭与你分享每场 LeetCode 周赛的解题报告，一起体会上分之旅。

本文是 LeetCode 上分之旅系列的第 48 篇文章，往期回顾请移步到文章末尾~

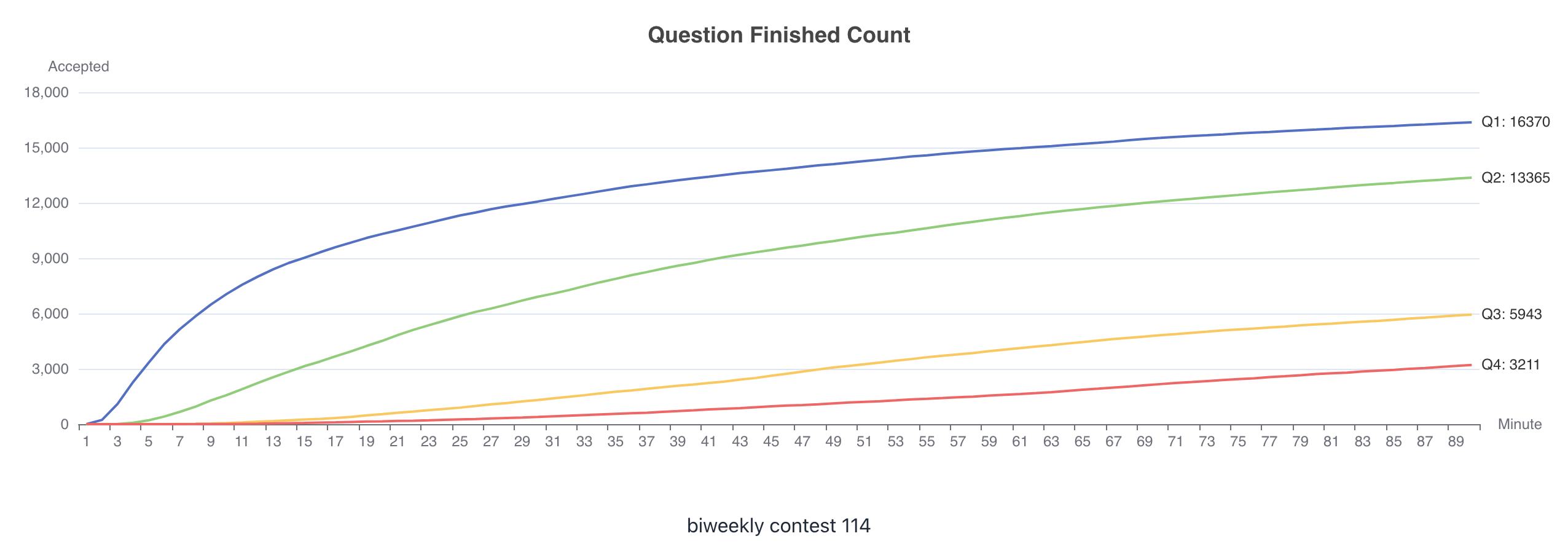
LeetCode 双周赛 114

T1. 收集元素的最少操作次数（Easy）

• 标签：模拟、散列表

T2. 使数组为空的最少操作次数（Medium）

• 标签：贪心、散列表

T3. 将数组分割成最多数目的子数组（Medium）

• 标签：思维、位运算

T4. 可以被 K 整除连通块的最大数目（Hard）

• 标签：树上 DP

---

T1. 收集元素的最少操作次数（Easy）

https://leetcode.cn/problems/minimum-operations-to-collect-elements/description/

题解（散列表)

简单模拟题。

预初始化包含 $1-k$ 元素的集合，根据题意逆向遍历数组并从集合中移除元素，当集合为空时表示已经收集到所有元素，返回 $n-i$。

class Solution {fun minOperations(nums: List<Int>, k: Int): Int {val n = nums.sizeval set = (1..k).toHashSet()for (i in n - 1 downTo 0) {set.remove(nums[i])if (set.isEmpty()) return n - i}return -1}
}

class Solution:def minOperations(self, nums, k):n, nums_set = len(nums), set(range(1, k+1))for i in range(n-1, -1, -1):nums_set.discard(nums[i])if not nums_set:return n - ireturn -1

class Solution {
public:int minOperations(std::vector<int>& nums, int k) {int n = nums.size();unordered_set<int> set;for (int i = 1; i <= k; ++i) {set.insert(i);}for (int i = n - 1; i >= 0; --i) {set.erase(nums[i]);if (set.empty()) {return n - i;}}return -1;}
};

function minOperations(nums: number[], k: number): number {var n = nums.length;var set = new Set<number>();for (let i = 1; i <= k; ++i) {set.add(i);}for (let i = n - 1; i >= 0; --i) {set.delete(nums[i]);if (set.size === 0) {return n - i;}}return -1;
};

class Solution {int minOperations(List<int> nums, int k) {int n = nums.length;Set<int> set = Set<int>();for (int i = 1; i <= k; i++) {set.add(i);}for (int i = n - 1; i >= 0; i--) {set.remove(nums[i]);if (set.isEmpty) return n - i;}return -1;}
}

复杂度分析：

• 时间复杂度：$O(n)$ 线性遍历；
• 空间复杂度：$O(k)$ 散列表空间。

---

T2. 使数组为空的最少操作次数（Medium）

https://leetcode.cn/problems/minimum-number-of-operations-to-make-array-empty/description/

题解（贪心）

题目两种操作的前提是数字相等，因此我们先统计每个元素的出现次数。

从最少次数的目标出发，显然能移除 $3$ 个就尽量移除 $3$ 个，再分类讨论：

• 如果出现次数为 $1$，那么一定无解，返回 $-1$；
• 如果出现次数能够被 $3$ 整除，那么操作 $cnt/3$ 次是最优的；
• 如果出现次数除 $3$ 余 $1$，那么把 $1$ 个 $3$ 拆出来合并为 4，操作 $cnt/3+1$ 次是最优的；
• 如果出现次数除 $3$ 余 $2$，那么剩下的 $2$ 操作 $1$ 次，即操作 $cnt/3+1$ 次是最优的。

组合以上讨论：

class Solution {fun minOperations(nums: IntArray): Int {val cnts = HashMap<Int, Int>()for (e in nums) {cnts[e] = cnts.getOrDefault(e, 0) + 1}var ret = 0for ((_, cnt) in cnts) {if (cnt == 1) return -1when (cnt % 3) {0 -> {ret += cnt / 3}1, 2 -> {ret += cnt / 3 + 1}}}return ret}
}

继续挖掘题目特性，对于余数大于 $0$ 的情况总是 向上取整 ，那么可以简化为：

class Solution {fun minOperations(nums: IntArray): Int {val cnts = HashMap<Int, Int>()for (e in nums) {cnts[e] = cnts.getOrDefault(e, 0) + 1}var ret = 0for ((_, cnt) in cnts) {if (cnt == 1) return -1ret += (cnt + 2) / 3 // 向上取整}return ret}
}

class Solution:def minOperations(self, nums: List[int]) -> int:cnts = Counter(nums)ret = 0for cnt in cnts.values():if cnt == 1: return -1ret += (cnt + 2) // 3return ret

class Solution {
public:int minOperations(std::vector<int>& nums) {unordered_map<int, int> cnts;for (auto &e : nums) {cnts[e] += 1;}int ret = 0;for (auto &p: cnts) {if (p.second == 1) return -1;ret += (p.second + 2) / 3;}return ret;}
};

function minOperations(nums: number[]): number {let cnts: Map<number, number> = new Map<number, number>();for (let e of nums) {cnts.set(e, (cnts.get(e) ?? 0) + 1);}let ret = 0;for (let [_, cnt] of cnts) {if (cnt == 1) return -1;ret += Math.ceil(cnt / 3);}return ret;
};

class Solution {int minOperations(List<int> nums) {Map<int, int> cnts = {};for (int e in nums) {cnts[e] = (cnts[e] ?? 0) + 1;}int ret = 0;for (int cnt in cnts.values) {if (cnt == 1) return -1;ret += (cnt + 2) ~/ 3; // 向上取整}return ret;}
}

复杂度分析：

• 时间复杂度：$O(n)$ 线性遍历
• 空间复杂度：$O(n)$ 计数空间。

---

T3. 将数组分割成最多数目的子数组（Medium）

https://leetcode.cn/problems/split-array-into-maximum-number-of-subarrays/description/

题解（思维题）

一个重要的结论是：当按位与的数量增加时，按位与的结果是非递增的。

题目要求在子数组的按位与的和最小的前提下，让子数组的个数最大。根据上面的结论，显然将数组全部按位与是最小的。

分类讨论：

• 如果整体按位于的结果不为 $0$，那么就不可能存在分割数组的方法使得按位与的和更小，直接返回 $1$；
• 否则，问题就变成分割数组的最大个数，使得每个子数组按位与为 $0$，直接贪心分割就好了。

class Solution {fun maxSubarrays(nums: IntArray): Int {val mn = nums.reduce { acc, it -> acc and it }if (mn > 0) return 1 // 特判var ret = 0var cur = Integer.MAX_VALUEfor (i in nums.indices) {cur = cur and nums[i]if (cur == 0) {cur = Integer.MAX_VALUEret++}}return ret }
}

class Solution:def maxSubarrays(self, nums: List[int]) -> int:if reduce(iand, nums): return 1ret, mask = 0, (1 << 20) - 1cur = maskfor num in nums:cur &= numif cur == 0: ret += 1; cur = maskreturn ret

class Solution {
public:int maxSubarrays(vector<int>& nums) {int mn = nums[0];for (auto num : nums) mn &= num;if (mn != 0) return 1;int ret = 0;int cur = INT_MAX;for (int i = 0; i < nums.size(); i++) {cur &= nums[i];if (cur == 0) {cur = INT_MAX;ret++;}}return ret;}
};

function maxSubarrays(nums: number[]): number {const n = nums.length;let mn = nums.reduce((acc, it) => acc & it);if (mn > 0) return 1; // 特判let mask = (1 << 20) - 1let ret = 0;let cur = mask;for (let i = 0; i < n; i++) {cur = cur & nums[i];if (cur === 0) {cur = mask;ret++;}}return ret;
};

class Solution {int maxSubarrays(List<int> nums) {var mn = nums.reduce((acc, it) => acc & it);if (mn > 0) return 1; // 特判var mask = (1 << 20) - 1;var ret = 0;var cur = mask;for (var i = 0; i < nums.length; i++) {cur = cur & nums[i];if (cur == 0) {cur = mask;ret++;}}return ret;}
}

复杂度分析：

• 时间复杂度：$O(n)$ 线性遍历；
• 空间复杂度：$O(1)$ 仅使用常量级别空间。

---

T4. 可以被 K 整除连通块的最大数目（Hard）

https://leetcode.cn/problems/maximum-number-of-k-divisible-components/

问题分析

初步分析：

• 问题目标： 求解分割后满足条件的最大连通块数量；
• 问题条件： 连通块的和能够被 K 整除；
• 关键信息： 题目保证数据是可以分割的，这是重要的前提。

思考实现：

在保证问题有解的情况下，树上的每个节点要么是单独的连通分量，要么与邻居组成连通分量。那么，这就是典型的「连或不连」和「连哪个」动态规划思维。

• 思考「连或不连」：

如果节点 $A$ 的价值能够被 $K$ 整除，那么节点 $A$ 能作为单独的连通分量吗？

不一定，例如 $K=3$ 且树为 $1-3-5$ 的情况，连通分量只能为 $1$，因为 $3$ 左右子树都不能构造合法的连通块，因此需要与 $3$ 连接才行。

• 继续思考「连哪个」：

那么，节点 $A$ 应该与谁相连呢？对于节点 $A$ 的某个子树 $Tre{e}_i$ 来说，存在 $2$ 种情况：

• 能整除：那么子树 $Tre{e}_i$ 不需要和节点 $A$ 相连；
• 不能整除：那么子树 $Tre{e}_i$ 的剩余值就必须与节点 $A$ 相连，有可能凑出 $K$ 的整除。

当节点 $A$ 与所有子树的剩余值组合后，再加上当前节点的价值，如果能够构造出 $K$ 的整数倍时，说明找到一个新的连通块，并且不需要和上一级节点组合。否则，则进入不能整除的条件，继续和上一级节点组合。

题解（DFS）

• 定义 DFS 函数并返回两个数值：<子树构造的连通分量, 剩余值>；
• 任意选择一个节点为根节点走一遍 DFS，最终返回 $dfs(0,-1)[0]$。

class Solution {fun maxKDivisibleComponents(n: Int, edges: Array<IntArray>, values: IntArray, k: Int): Int {// 建图val graph = Array(n) { LinkedList<Int>() }for ((u, v) in edges) {graph[u].add(v)graph[v].add(u)}// DFS <cnt, left>fun dfs(i: Int, pre: Int): IntArray {var ret = intArrayOf(0, values[i])for (to in graph[i]) {if (to == pre) continueval (childCnt, childLeft) = dfs(to, i)ret[0] += childCntret[1] += childLeft}if (ret[1] % k == 0) {ret[0] += 1ret[1] = 0}return ret}return dfs(0, -1)[0]}
}

class Solution:def maxKDivisibleComponents(self, n, edges, values, k):# 建图graph = defaultdict(list)for u, v in edges:graph[u].append(v)graph[v].append(u)# DFS <cnt, left>def dfs(i, pre):ret = [0, values[i]]for to in graph[i]:if to == pre: continuechildCnt, childLeft = dfs(to, i)ret[0] += childCntret[1] += childLeftif ret[1] % k == 0:ret[0] += 1ret[1] = 0return retreturn dfs(0, -1)[0]

class Solution {
public:int maxKDivisibleComponents(int n, vector<vector<int>>& edges, vector<int>& values, int k) {// 建图vector<list<int>> graph(n);for (auto& edge : edges) {int u = edge[0];int v = edge[1];graph[u].push_back(v);graph[v].push_back(u);}// DFS <cnt, left>function<vector<int>(int, int)> dfs = [&](int i, int pre) -> vector<int> {vector<int> ret(2, 0);ret[1] = values[i];for (int to : graph[i]) {if (to == pre) continue;vector<int> child = dfs(to, i);ret[0] += child[0];ret[1] += child[1];}if (ret[1] % k == 0) {ret[0] += 1;ret[1] = 0;}return ret;};return dfs(0, -1)[0];}
};

function maxKDivisibleComponents(n: number, edges: number[][], values: number[], k: number): number {// 建图let graph = Array(n).fill(0).map(() => []);for (const [u, v] of edges) {graph[u].push(v);graph[v].push(u);}// DFS <cnt, left>let dfs = (i: number, pre: number): number[] => {let ret = [0, values[i]];for (let to of graph[i]) {if (to === pre) continue;let [childCnt, childLeft] = dfs(to, i);ret[0] += childCnt;ret[1] += childLeft;}if (ret[1] % k === 0) {ret[0] += 1;ret[1] = 0;}return ret;};return dfs(0, -1)[0];  
};

class Solution {int maxKDivisibleComponents(int n, List<List<int>> edges, List<int> values, int k) {// 建图List<List<int>> graph = List.generate(n, (_) => []);for (final edge in edges) {int u = edge[0];int v = edge[1];graph[u].add(v);graph[v].add(u);}// DFS <cnt, left>List<int> dfs(int i, int pre) {List<int> ret = [0, values[i]];for (int to in graph[i]) {if (to == pre) continue;List<int> child = dfs(to, i);ret[0] += child[0];ret[1] += child[1];}if (ret[1] % k == 0) {ret[0] += 1;ret[1] = 0;}return ret;}return dfs(0, -1)[0];}
}

复杂度分析：

• 时间复杂度：$O(n)$ 每个节点访问 $1$ 次；
• 空间复杂度：$O(n)$ 图空间。

推荐阅读

LeetCode 上分之旅系列往期回顾：

• LeetCode 单周赛第 364 场 · 前后缀分解结合单调栈的贡献问题
• LeetCode 单周赛第 363 场 · 经典二分答案与质因数分解
• LeetCode 双周赛第 113 场 · 精妙的 O(lgn) 扫描算法与树上 DP 问题
• LeetCode 双周赛第 112 场 · 计算机科学本质上是数学吗？

⭐️ 永远相信美好的事情即将发生，欢迎加入小彭的 Android 交流社群~