---

一、题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大**（一个节点也可以是它自己的祖先）**。”

示例 1

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2

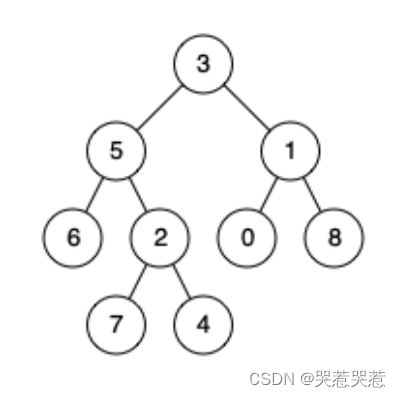
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3

输入：root = [1,2], p = 1, q = 2
输出：1

提示：
树中节点数目在范围 [2, 10^5] 内。
-10^9 <= Node.val <= 10^9
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

二、代码

代码如下：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':p_father = []q_father = []def findp(r,path):if r.val == p.val:p_father.extend(path)p_father.append(r)returnif r.left != None:path.append(r)findp(r.left,path)path.pop()if r.right != None:path.append(r)findp(r.right,path)path.pop()def findq(r,path):if r.val == q.val:q_father.extend(path)q_father.append(r)returnif r.left != None:path.append(r)findq(r.left,path)path.pop()if r.right != None:path.append(r)findq(r.right,path)path.pop()findp(root,[])findq(root,[])presult = rootfor i in range(min(len(q_father),len(p_father))):if q_father[i] == p_father[i]:result = q_father[i]continueelse:breakreturn result

---

三、解题思路

本题在235. 二叉搜索树的最近公共祖先
的基础上将二叉搜索树改为二叉树，那么根据我们之前搜索p,q节点的所有父节点的思路来看，搜索方式有所不同，不能通过二叉搜索树的规律来快速找到对应p,q节点，但也可以通过一步一步试错的方式慢慢找到所有的父节点，解题思路同235. 二叉搜索树的最近公共祖先
一致，通过找出p，q节点所有的父节点列表，然后找出列表的最大公共子列表后，最后一个元素即为最近公共祖先。