郑州网站建设熊掌号公司做网站一般多少钱

剑指 Offer 42. 连续子数组的最大和

难度：$easy$

---

题目描述

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

要求时间复杂度为O(n)。

示例1:

输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

提示：

• $1<=arr.length<=10^5$
• $-100<=arr[i]<=100$

注意：本题与主站 53 题相同：https://leetcode-cn.com/problems/maximum-subarray/

---

算法

常见解法	时间复杂度
暴力搜索	$O(n^2)$
分治思想	$O(nlogn)$
动态规划	$O(n)$

(动态规划)

• 状态定义： 设动态规划列表 $dp$ ，$dp[i]$ 代表以元素 $nums[i]$ 为结尾的连续子数组最大和。

为何定义最大和 dp[i] 中必须包含元素 nums[i] ：保证 dp[i] 递推到 dp[i+1] 的正确性；如果不包含 nums[i] ，递推时则不满足题目的 连续子数组 要求。

• 转移方程： 若 $dp[i-1]\le 0$ ，说明 $dp[i-1]$ 对 $dp[i]$ 产生负贡献，即 $dp[i-1]+nums[i]$ 还不如 $nums[i]$ 本身大。

  • 当 $dp[i-1]>0$ 时：执行 $dp[i]=dp[i-1]+nums[i]$ ；
  • 当 $dp[i-1]\le 0$ 时：执行 $dp[i]=nums[i]$ ；

• 初始状态： $dp[0]=nums[0]$，即以 $nums[0]$ 结尾的连续子数组最大和为 $nums[0]$ 。

• 返回值： 返回 $dp$ 列表中的最大值，代表全局最大值。

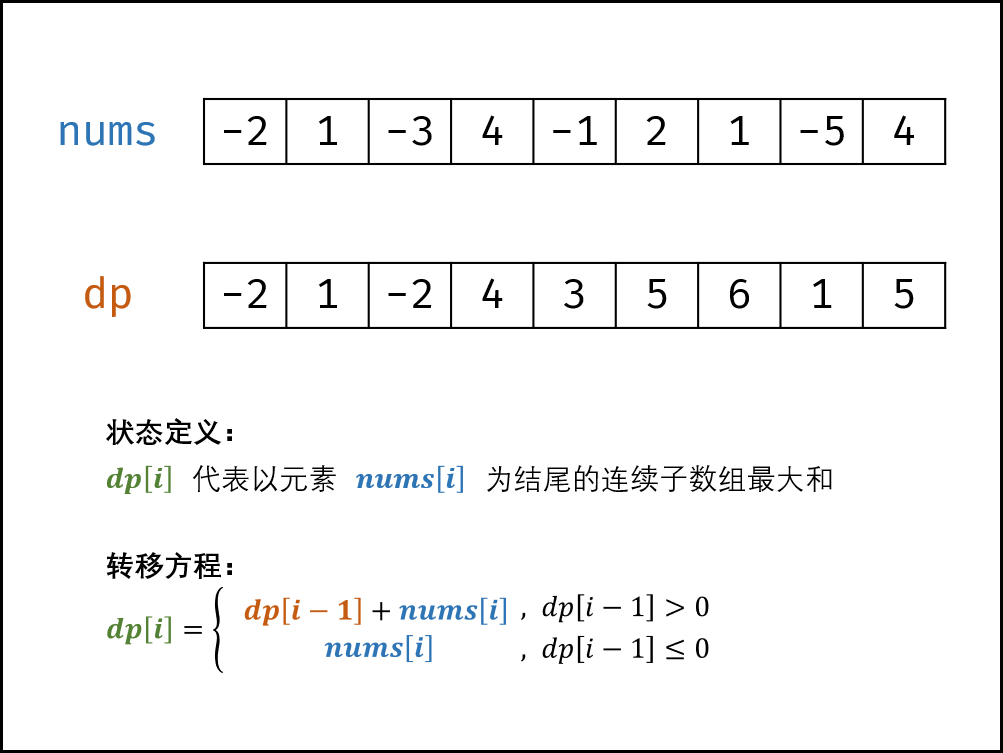
复杂度分析

• 时间复杂度：$O(n)$。

• 空间复杂度 : $O(1)$

C++ 代码

使用 res 代表最终的答案，s 表示前 i - 1 项的值， 如果前 i - 1 项的值小于 0，s 等于当前的数 num，如果大于 0， 说明可以加上当前的数字 num，继续往后运算。

class Solution {
public:int maxSubArray(vector<int>& nums) {int res = INT_MIN, s = 0;for (auto x : nums) {if (s < 0) s = 0;s += x;res = max(res, s);}return res;}
};

---

参考链接