做标书的网站5月新冠病毒最新消息
实验的目的和要求：通过本次实验使学生进一步熟悉掌握使用MATLAB软件，并能利用该软件进行无约束最优化方法的计算。
实验内容：
１、最速下降法的MATLAB实现
２、牛顿法的MATLAB实现
３、共轭梯度法的MATLAB实现
学习建议：
本次实验就是要通过对一些具体问题的分析进一步熟悉软件的操作并加深对理论知识的理解。
重点和难点：
通过同一个具体问题用不同的方法解决的比较，加深理解恰当选用优化问题解决方法的重要性。
一 最速下降法
1.最速下降法基本原理和步骤
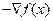思想：寻求最速下降方向即负梯度方向
MATLAB实现:
2.代码及数值算例:
(1) 程序源代码:
function [ X,FMIN,K ] = zuisuxiajiang( f,x,x0,e )% [ X,FMIN,N ] =zuisuxiajiang()法求解无约束问题% X 极小点% FMIN 极小值% K 迭代次数% f 问题函数% x 变量% x0 初始点% e 终止误差% 张超编写于2014/04/15 count=0;td=jacobian(f,x)';while norm(subs(td,x,x0))>eP=-subs(td,x,x0);syms ry=x0+r*P;ft(r)=subs(f,x,y); [r0]=fibonacci(ft,0,100,0.01);x0=x0+r0*P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
二 牛顿法
1.牛顿法基本原理和步骤
思想：在第k次迭代的迭代点x(k)邻域内，用一个二次函数（如二阶泰勒多项式）去近似代替原目标函数f(x)，然后求出该二次函数的极小点作为对原目标函数求优的下一个迭代点，依次类推，通过多次重复迭代，使迭代点逐步逼近原目标函数的极小点。
设*f(x)*二次连续可微，在点 x(k） 处的Hesse矩阵正定。
MATLAB实现:
2.代码及数值算例:
(2) 程序源代码:
function [ X,FMIN,K ] = ysNewton( f,x,x0,e )% [ X,FMIN,N ] =ysNewton()原始牛顿法求解无约束问题% X 极小点% FMIN 极小值% K 迭代次数% f 问题函数% x 变量% x0 初始点% e 终止误差% 张超编写于2014/04/15count=0;td=jacobian(f,x)';H=jacobian(td',x);while norm(subs(td,x,x0))>eP=-subs(H,x,x0)^(-1)*subs(td,x,x0);x0=x0+P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
牛顿法对于二次正定函数只需做一次迭代就得到最优解。特别在极小点附近，收敛性很好速度也很快。
但牛顿法也有缺点，它要求初始点离最优解不远，若初始点选的离最优解太远时，牛顿法并不能保证其收敛，甚至也不是下降方向。
为了克服牛顿法的缺点，人们保留了从牛顿法中选取牛顿方向作为搜索方向，摒弃其步长恒取1的作法，而用一维搜索确定最优步长来构造算法。
(3) 程序源代码:
function [ X,FMIN,K ] = xzNewton( f,x,x0,e )% [ X,FMIN,N ] =xzNewton()带步长牛顿法求解无约束问题% X 极小点% FMIN 极小值% K 迭代次数% f 问题函数% x 变量% x0 初始点% e 终止误差% 张超编写于2014/04/15count=0;td=jacobian(f,x)';H=jacobian(td',x);while norm(subs(td,x,x0))>eP=-subs(H,x,x0)^(-1)*subs(td,x,x0);syms ry=x0+r*P;ft(r)=subs(f,x,y); [r0]=fibonacci(ft,0,100,0.01);x0=x0+r0*P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
三 共轭梯度法
1.共轭梯度法基本原理和步骤
思想：将共轭性和最速下降方向相结合，利用已知迭代点处的梯度方向构造一组共轭方向，并沿此方向进行搜索，求出函数的极小点。
MATLAB实现:
2.代码及数值算例:
(1) 程序源代码:
function [ X,FMIN,K ] = gongetidu( f,x,x0,e )% [ X,FMIN,N ] =gongetidu()共轭梯度法求解无约束问题% X 极小点% FMIN 极小值% K 迭代次数% f 问题函数% x 变量% x0 初始点% e 终止误差% 张超编写于2014/04/15count=1;td=jacobian(f,x)';H=jacobian(td',x);if norm(subs(td,x,x0))>eP=-subs(td,x,x0);r0=-subs(td,x,x0)'*P/(P'*H*P);x0=x0+r0*P;else x0;endwhile norm(double(subs(td,x,x0)))>eb0=subs(td,x,x0)'*subs(td,x,x0)/(P'*P);P=-subs(td,x,x0)+b0*P;r0=-subs(td,x,x0)'*P/(P'*H*P);x0=x0+r0*P;count=count+1;endX=x0;FMIN=subs(f,x,x0);K=count;end
四 一个算例
分别用上述三中方法计算下题,并比较各算法.
Min f(x)=(x1 - 2)^2 + (x1 – 2*x2)^2
初始点x0=(0,3)T
允许误差e=0.1
键入命令并输出结果：
syms x1 x2\>> f=(x1-2)^2+(x1-2*x2)^2;\>> x=[x1;x2];\>> x0=[0;3];\>> e=0.1;[X,FMIN,N]=zuisuxiajiang(f,x,x0,e)X =1.97630.9818FMIN =7.2076e-04N =10\>> [X,FMIN,N]=ysNewton(f,x,x0,e)X =21FMIN =0N =1[X,FMIN,N]=gongetidu(f,x,x0,e)X =21FMIN =0N =2
由上述结果我们发现：
对于二次正定函数newton法只需一次迭代就得到正确结果，共轭梯度法只需进行两次（因为目标函数是二元函数）迭代就得出正确结果。但最速下降法却迭代了10次，虽然一维搜索存在误差，但实际上最速下降法也需迭代多次。