网站做1920px好吗华为手机业务最新消息
总的链接 :
面试经典 150 题 - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台
二分算法模板 :
详见 :
基础二分学习笔记-CSDN博客
35 . 搜索插入位置
链接 :
. - 力扣(LeetCode)
思路 :
用二分查找第一个>=target的下标 ;
这里就用最小化查找 , 即可 ;
class Solution {
public:int searchInsert(vector<int>& nums, int target) {// 第一个 >= target 的下标int n = nums.size() ;int l = -1 , r = n ;while(l + 1 < r){// l + 1 == n 结束int mid = l + r >> 1 ;if(nums[mid]>=target) r = mid ;else l = mid ;}// nums[r] ;return r ; }
};74 . 搜索二维矩阵
链接 :
. - 力扣(LeetCode)
LC题解链接 :
. - 力扣(LeetCode)
思路 :
既然是一个有序表 , 二维矩阵直接当成一维数组做 , 例如下标x 对应二维矩阵中的matrix[x/n][x%n] , 应用最小化二分查找, 找到第一个大于等于target的下标 , 最后判断一下 , 看找到下标的元素值是否为target , 是的话就返回true , 不是的话 , 返回false ;
代码 :
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size(), n = matrix[0].size();int l = -1 , r = m * n ;while(l+1<r){// 找到第一个 >=target 的下标int mid = (l + r) >> 1 ;int x = matrix[mid/n][mid%n] ;if(x>=target) r = mid ;else l = mid ;}// 右边是可行区域if(r!=m*n && matrix[r/n][r%n] == target) return true ;else return false;}
};162 . 寻找峰值 :
链接 :
. - 力扣(LeetCode)
正解:
二分 ,
数组可能存在许多个区间峰值 , 但是我们可以用二分找到整个数组的峰值 ;
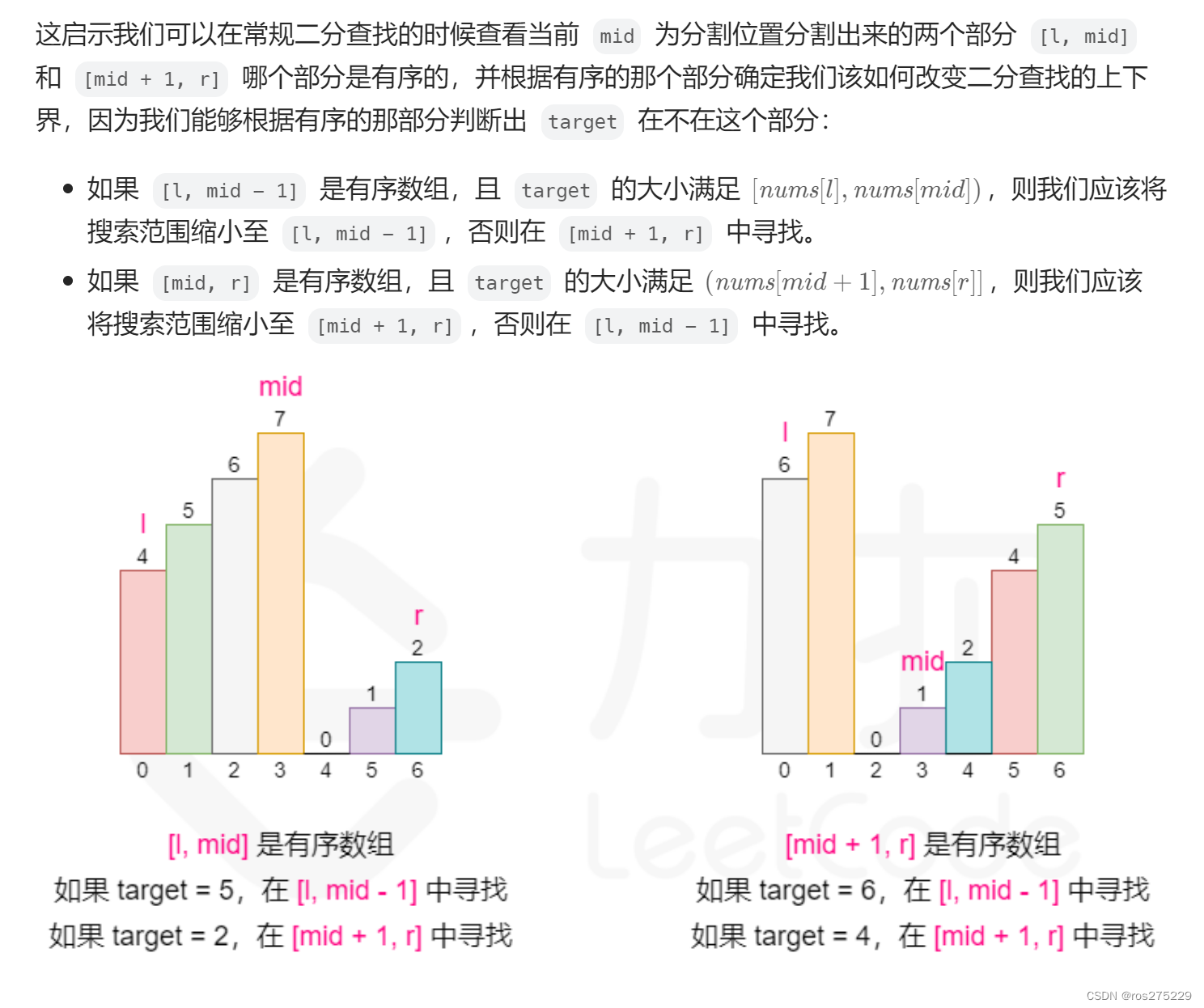
如果nums[mid] > nums[mid+1] , 那么我们可以使r = mid ;
否则的话 , l = mid + 1 ;
class Solution {
public:int findPeakElement(vector<int>& nums) {int n = nums.size() ;if(n==1) return 0 ;int l = 0 , r = n - 1;while(l < r){int mid = l + r >> 1 ;if(nums[mid] > nums[mid + 1]) r = mid ;else l = mid + 1 ;}return r ;}
};歪解 :
直接调用库函数求解 :
class Solution {
public:int findPeakElement(vector<int>& nums) {return max_element(nums.begin(),nums.end())-nums.begin();}
};33 . 搜索旋转排序数组
链接
. - 力扣(LeetCode)
思路 :
将数组从中间分开成左右两部分的时候,一定有一部分的数组是有序的。
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = (left + right) >> 1;if (nums[mid] == target) return mid;if (nums[left] <= nums[mid]) {// left 到 mid 是顺序区间(target >= nums[left] && target < nums[mid]) ? right = mid - 1 : left = mid + 1;}else {// mid 到 right 是顺序区间(target > nums[mid] && target <= nums[right]) ? left = mid + 1 : right = mid - 1;}}return -1;}
};34. 在排序数组中查找元素的第一个和最后一个位置
链接 :
. - 力扣(LeetCode)
思路 :
二分查找 ;
直接套用模板进行二分查找 ;
先找到第一个>=target的元素下标作为左边界, 找到最后一个<=target的下标作为右边界;
最后进行一下边界判断即可 ;
class Solution {
public:int findr(vector<int>& nums, int n ,int target){// 查找最后一个<=target的下标int l = -1 , r = n ;while(l + 1 < r){int mid = (l + r) >> 1 ;if(nums[mid]<=target) l = mid ;else r = mid ;}return l ;}int findl(vector<int>& nums, int n ,int target){//查找第一个>=target的下标int l = -1 , r = n ;while(l + 1 < r){int mid= (l + r) >> 1;if(nums[mid]>=target) r = mid ;else l = mid ;}return r ;} vector<int> searchRange(vector<int>& nums, int target) {int n = nums.size() ;if(n==0){return {-1,-1} ;}int l = findl(nums , n , target);int r = findr(nums, n , target);if(l>=0 && l < n && nums[l]==target){return {l,r};}else{return {-1,-1} ;}}
};153. 寻找旋转排序数组中的最小值
链接 :
. - 力扣(LeetCode)
思路 :
首先设置两个指针l, r;先写二分 :
// 左边界l,右边界r;
// 那么最小值一定会在[l,r]这个区间中 ;
// case 1 : nums[mid] < nums[r] : 说明nums[mid]是最小值右侧元素
// cese 2 : nums[mid] > nums[r] : 说明nums[mid]是最小值左侧的元素
详细请看代码 :
代码 :
class Solution {
public:int findMin(vector<int>& nums) {int n = nums.size() ;int l = 0 , r = n - 1;// 双闭区间// 左边界l,右边界r;// 那么最小值一定会在[l,r]这个区间中 ;// case 1 : nums[mid] < nums[r] : 说明nums[mid]是最小值右侧元素// cese 2 : nums[mid] > nums[r] : 说明nums[mid]是最小值左侧的元素while(l < r){int mid = (l + r) >> 1 ;if(nums[mid] < nums[r]) r = mid ;else if(nums[mid] > nums[r]) l = mid + 1 ; }return nums[r] ;}
};