一.qsort函数是什么

stdlib.h头文件下的函数

qsort()函数：是八大排序算法中的快速排序，能够排序任意数据类型的数组其中包括整形，浮点型，字符串甚至还有自定义的结构体类型。qsort函数实现对不同元素的排序主要就是通过对compar函数进行定义实现的，对于每一种变量类型的排序，我们都需要重新实现一种compar函数。

qsort函数是根据二分法写的，其时间复杂度为n*log(n)。

快速排序是对冒泡排序的一种改进。它的基本思想是∶通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

排序原理︰

1.首先设定一个分界值，通过该分界值将数组分成左右两部分;

2将大于或等于分界值的数据放到到数组右边，小于分界值的数据放到数组的左边。此时左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值;

3.然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。

4.重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左侧和右侧两个部分的数据排完序后，整个数组的排序也就完成了。

图解:

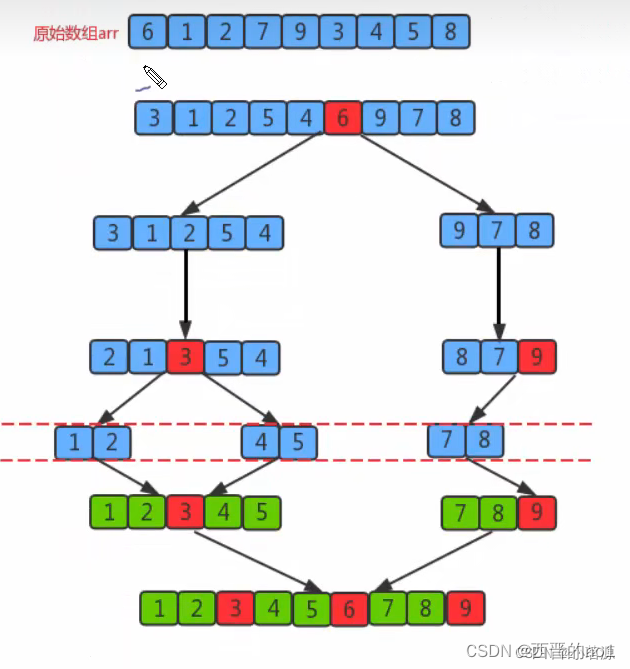
切分原理:

把一个数组切分成两个子数组的基本思想∶

1.找一个基准值，用两个指针分别指向数组的头部和尾部;

2.先从尾部向头部开始搜索一个比基准值小的元素，搜索到即停止，并记录指针的位置;

3.再从头部向尾部开始搜索一个比基准值大的元素，搜索到即停止，并记录指针的位置;

4.交换当前左边指针位置和右边指针位置的元素;

5.重复2,3,4步骤，直到左边指针的值大于右边指针的值停止。

图解:

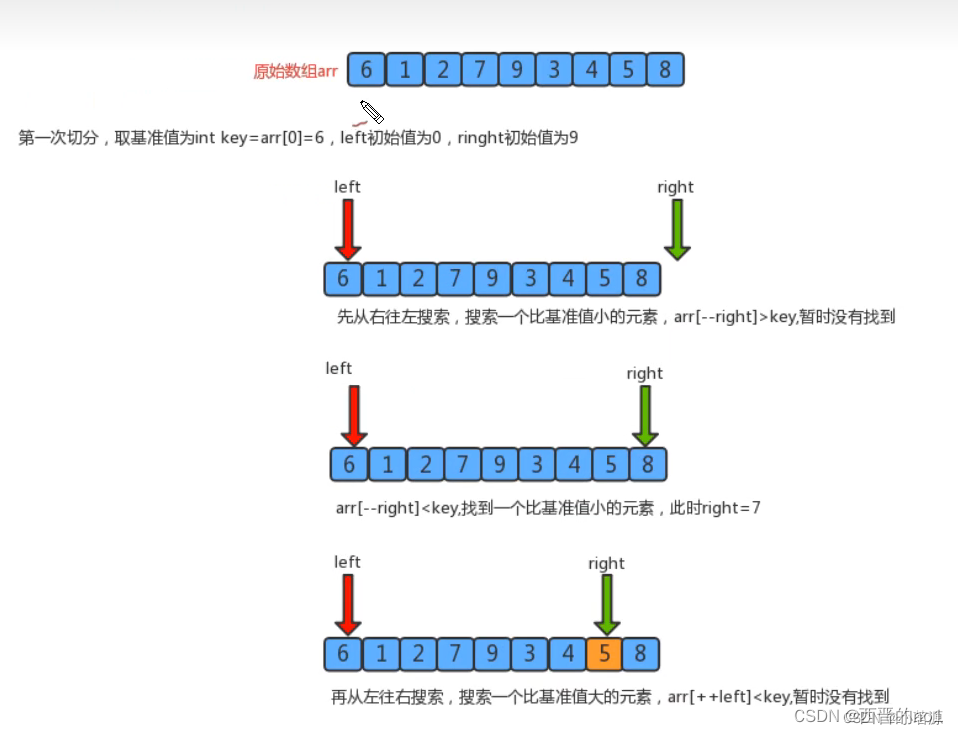
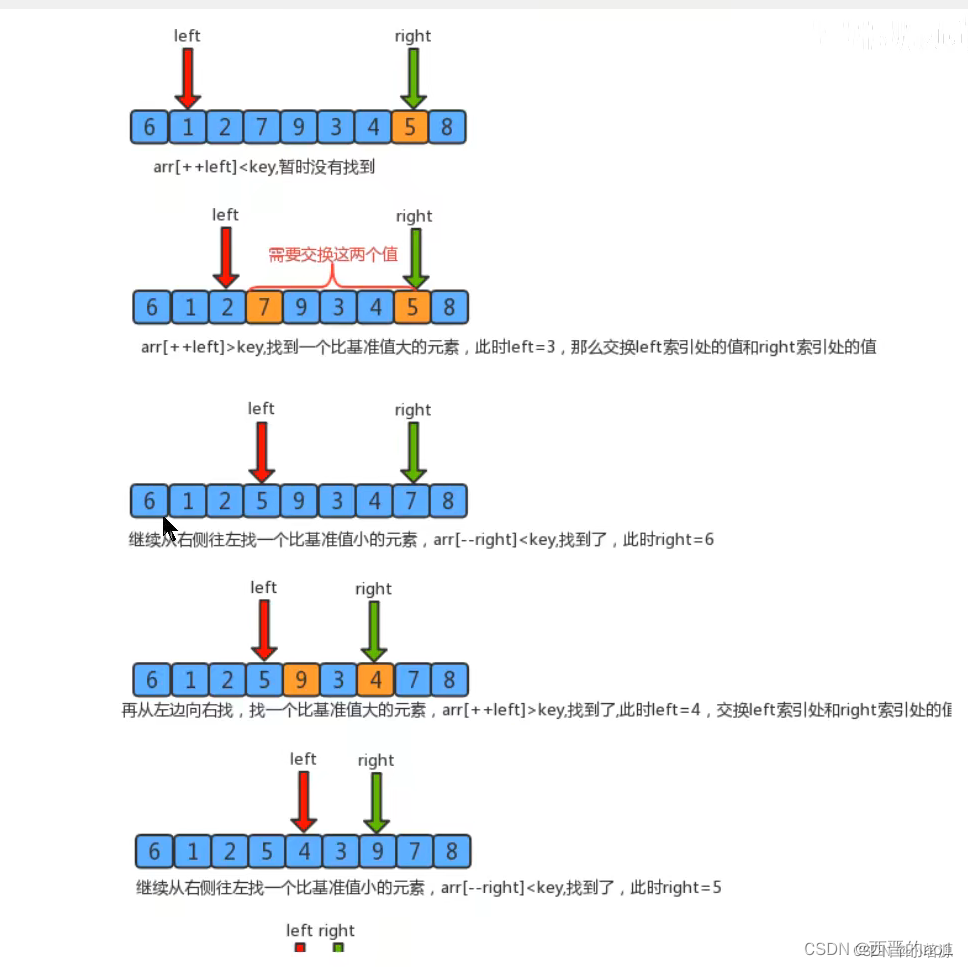
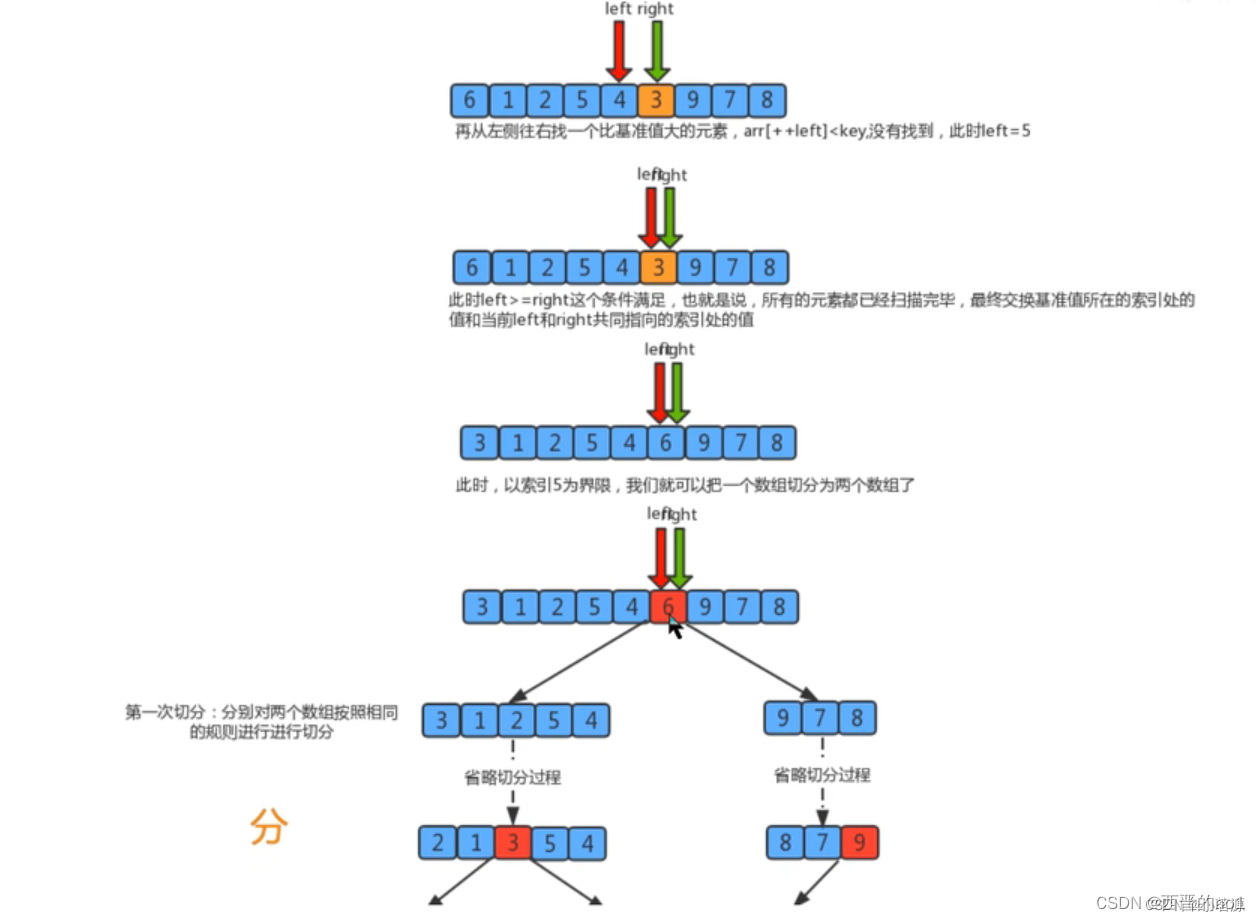
快速排序和归并排序的区别:

快速排序是另外一种分治的排序算法，它将一个数组分成两个子数组，将两部分独立的排序。快速排序和归并排序是互补的∶归并排序将数组分成两个子数组分别排序，并将有序的子数组归并从而将整个数组排序，而快速排序的方式则是当两个数组都有序时，整个数组自然就有序了。在归并排序中，一个数组被等分为两半，归并调用发生在处理整个数组之前，在快速排序中，切分数组的位置取决于数组的内容，递归调用发生在处理整个数组之后。

快速排序时间复杂分析:

快速排序的一次切分从两头开始交替搜索，直到left和right重合，因此，一次切分算法的时间复杂度为o(n),但整个快速排序的时间复杂度和切分的次数相关。

最优情况∶每一次切分选择的基准数字刚好将当前序列等分。

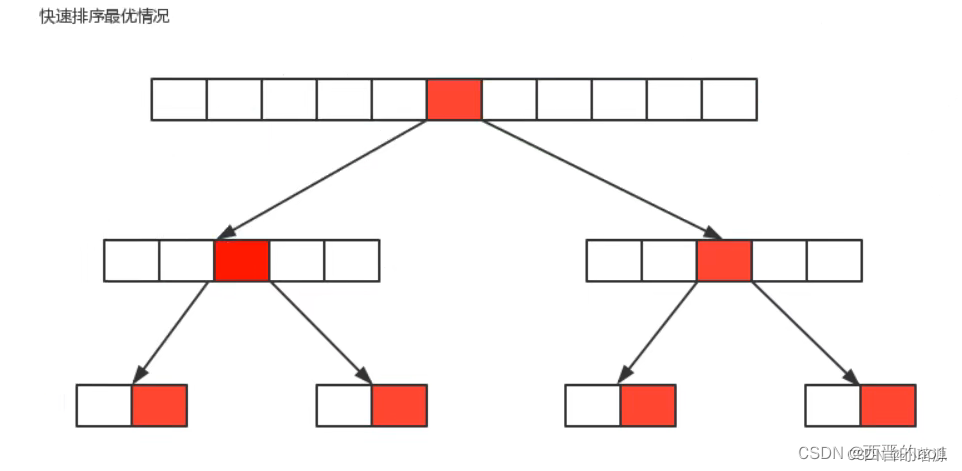
如果我们把数组的切分看做是一个树，那么上图就是它的最优情况的图示，共切分了]o:n次，所以，最优情况下快速排序的时间复杂度为O(nlogn)

最坏情况∶每一次切分选择的基准数字是当前序列中最大数或者最小数，这使得每次切分都会有一个子组，那么总共就得切分n次，所以，最坏情况下，快速排序的时间复杂度为O(n个2);

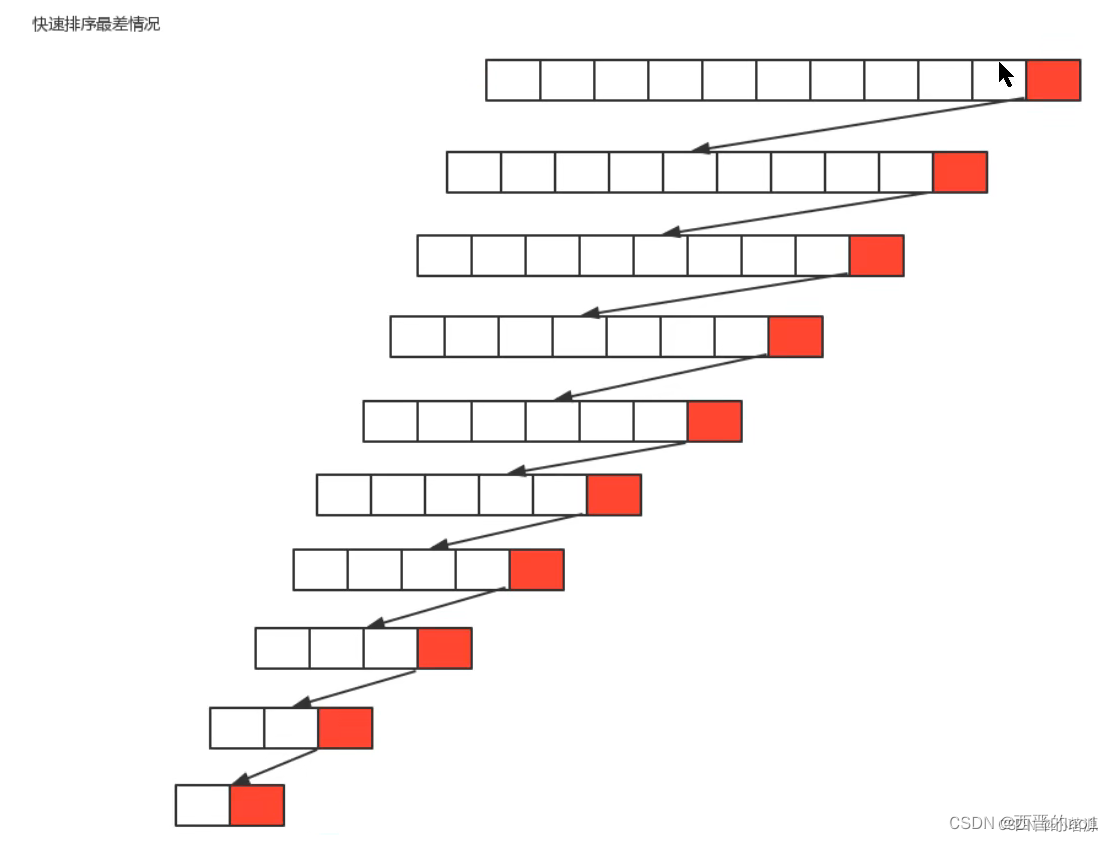
平均情况:每一次切公选择的甚准数字不具最大值和最小值，也不是中值，这种情况我们也可以用数学归纳法证明，快速排序的时间复杂度为o(nlogn).由于数学归纳法有很多数学相关的知识，容易使我们混抡，所以这里就不对平均情况的时间复杂度做证明了。

排序的稳定性:

稳定性的定义:

数组arr中有若干元素，其中A元素和B元素相等。并且A元素在B元素前面,如果使用某种排序算法排序后，能够保证A元素依然在B元,素的前面，可以说这个该算法是稳定的。

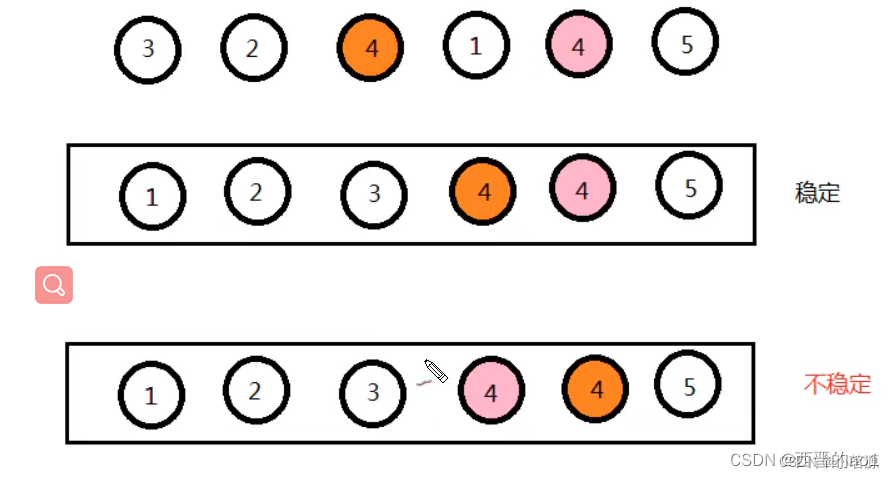
稳定性的意义:

如果一组数据只需要一次排序，则稳定性一般是没有意义的，如果一组数据需要多次排序，稳定性是有意义的。例如要排序的内容是一组商品对象，第一次排序按照价格由低到高排序，第二次排序按照销量由高到低排序，如果第二次排序使用稳定性算法，就可以使得相同销量的对象依旧保持着价格高低的顺序展现，只有销量不同的对象才需要重新排序。这样既可以保持第一次排序的原有意义，而且可以减少系统开销。

常见排序算法的稳定性:

冒泡排序:

只有当arr[i]>arr[i+1]的时候，才会交换元素的位置，而相等的时候并不交换位置，所以冒泡排序是一种稳定排序算法。

选择排序:

选择排序是给每个位置选择当前元素最小的,，例如有数据{5(1)，8，5(2)，2，9},第一遍选择到的最小元素为2

所以5(1)会和2进行交换位置，此时5(1)到了5(2)后面，破坏了稳定性，所以选择排序是一种不稳定的排序算法。

插入排序︰

比较是从有序序列的末尾开始，也就是想要插入的元素和已经有序的最大者开始比起，如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的，那么把要插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

希尔排序:

希尔排序是按照不同步长对元素进行插入排序,虽然一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以希尔排序是不稳定的。

归并排序:

归并排序在归并的过程中，只有arrli]arr[i+1]的时候才会交换位置，如果两个元素相等则不会交换位置，所以它并不会破坏稳定性，归并排序是稳定的。

快速排序︰

希尔排序是按照不同步长对元素进行插入排序,虽然一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以希尔排序是不稳定的。

归并排序:

归并排序在归并的过程中，只有arrli]arr[i+1]的时候才会交换位置，如果两个元素相等则不会交换位置，所以它并不会破坏稳定性，归并排序是稳定的。

快速排序︰

快速排序需要一个基准值，在基准值的右侧找一个比基准值小的元素，在基准值的左侧找一个比基准值大的元素，然后交换这两个元素，此时会破坏稳定性，所以快速排序是一种不稳定的算法。

qsort函数参数说明：

void qsort (

void* base, // 需要排序的目标数组名（或者也可以理解成开始排序的地址，可以写&s[i]这样的表达式）

size_t num, // 第二个参数 num 是参与排序的目标数组元素个数

size_t size, // 单个元素的大小（或者目标数组中每一个元素长度）,单位是字节，推荐使用sizeof(s[0]）这样的表达式 int(*compar)(const void* e1, const void* e2) // 比较函数

);

没有返回值。

其中compar是函数指针，compar指向的是：排序时，用来比较两个元素的函数。需要自己编写。

compar比较函数可以随便写成什么名字，如cmp

典型的cmp的定义是int cmp(const void *a,const void *b);

返回值必须是int，如果不是一定要强制类型转换成int，两个参数的类型必须都是const void *，a, b是随便写的，个人喜好。

返回值：<0(不进行置换)，>0(进行置换)，0(不进行置换)。

比较函数默认是升序排列，若想降序排列，交换函数实现里的a和b位置即可。

qsort算法不具有稳定性，排序时，相同大小元素相对位置可能会发生改变。

qsort只能针对不要求排序稳定性的场合使用，也即仅对元素排序，元素对应的位置没有意义。

假设是对int排序的话，如果是升序，那是a比b大返回一个正值，小则负值，相等返回0，其他的依次类推。

二.使用qsort排序-多个类型排序示例

#include <stdio.h>
#include <string.h>
#include <stdlib.h>// 注意类型时void* 所以要强制类型转化，还要解引用才是对应的值！！！// 要比较的数据是整形
int cmp_int(const void* a, const void* b)
{return *(int*)a - *(int*)b; // 升序排序 // return *(int *)b - *(int *)a; //降序排序
}// 要比较的数据是浮点型(float)
int cmp_float(const void* a, const void* b)
{//返回值的问题，显然cmp返回的是一个整型，所以避免float返回小数而被丢失(0.2 -0.1 = 0.1 强制类型转化为int后 结果为0)，用一个判断返回值。return (*(float*)a > *(float*)b) ? 1 : -1;
}// 要比较的数据是浮点型(double)
int cmp_double(const void* a, const void* b)
{//返回值的问题，显然cmp返回的是一个整型，所以避免double返回小数而被丢失(0.2 -0.1 = 0.1 强制类型转化为int后 结果为0)，用一个判断返回值。return (*(double*)a > *(double*)b) ? 1 : -1;
}// 要比较的数据是字符型(char),本质上是比较Ascii值
int cmp_char(const void* a, const void* b)
{return *(char*)a - *(char*)b;
}// 要比较的是字符串的字典顺序
int cmp_str_size(const void* a, const void* b)
{return strcmp((char*)a, (char*)b);
}// 要比较的是字符串的长度
int cmp_str_len(const void* a, const void* b)
{return strlen((char*)a) > strlen((char*)b) ? 1 : -1;
}// 要比较的数据是结构体变量
typedef struct stu
{// char name;int age;double weight;double hight;
}stu;
int cmp_by_weight(const void* a, const void* b)
{return (int)(((stu*)a)->weight - ((stu*)b)->weight);
}int main()
{int i;int arr_len;printf("对int型数组排序\n");int arr_int[] = { 1,2,3,4,5,9,8,7,6 };arr_len = sizeof(arr_int) / sizeof(int);for (i = 0; i < arr_len; i++)printf("%d  ", arr_int[i]);printf("\n");qsort(arr_int, arr_len, sizeof(arr_int[0]), cmp_int);for (i = 0; i < arr_len; i++)printf("%d  ", arr_int[i]);printf("\n\n");printf("对float型数组排序\n");float arr_float[] = { 1.1f,2.2f,3.3f,4.4f,5.5f,9.9f,8.8f,7.7f,6.6f };arr_len = sizeof(arr_float) / sizeof(float);for (i = 0; i < arr_len; i++)printf("%g  ", arr_float[i]);printf("\n");qsort(arr_float, arr_len, sizeof(arr_float[0]), cmp_float);for (i = 0; i < arr_len; i++)printf("%g  ", arr_float[i]);printf("\n\n");printf("对double型数组排序\n");double arr_double[] = { 1.1,2.2,3.3,4.4,5.5,9.9,8.8,7.7,6.6 };arr_len = sizeof(arr_double) / sizeof(double);for (i = 0; i < arr_len; i++)printf("%g  ", arr_double[i]);printf("\n");qsort(arr_double, arr_len, sizeof(arr_double[0]), cmp_double);for (i = 0; i < arr_len; i++)printf("%g  ", arr_double[i]);printf("\n\n");printf("对char型数组排序\n");char arr_char[] = "abcfed";arr_len = sizeof(arr_char) / sizeof(char) - 1;  // 因为sizeof把\0也算进去了，所以计算出来的值比字符串本身长度多1for (i = 0; i < arr_len; i++)printf("%c  ", arr_char[i]);printf("\n");qsort(arr_char, arr_len, sizeof(arr_char[0]), cmp_char);for (i = 0; i < arr_len; i++)printf("%c  ", arr_char[i]);printf("\n\n");printf("对字符串型数组按字典顺序排序-\n(字典序:对于字符串，先按首字符排序，如果首字符相同，再按第二个字符排序，以此类推。如aa, ab, ba, bb, bc就是一个字典序。)\n");
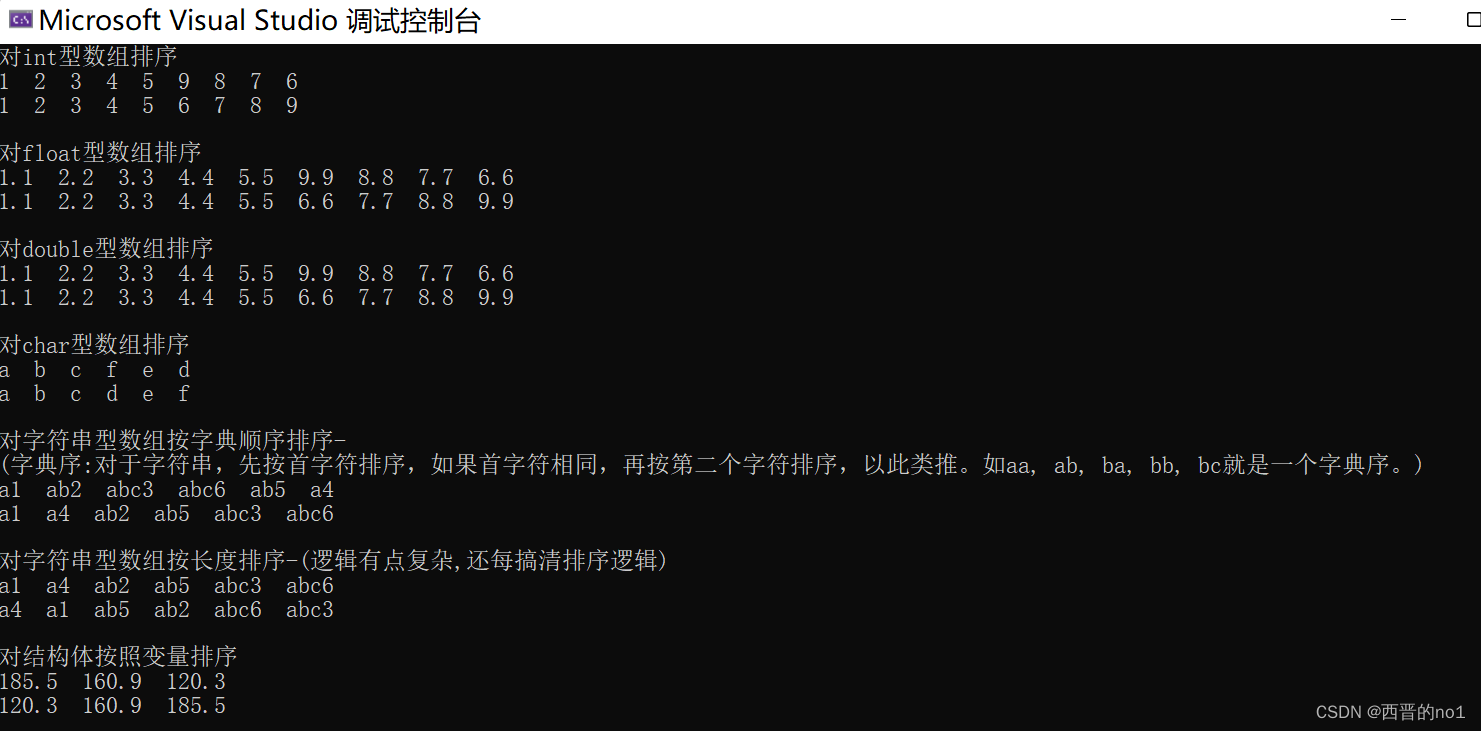
#define STR_SIZE 100char arr_str[][STR_SIZE] = { "a1","ab2","abc3","abc6","ab5" ,"a4" };arr_len = 6;for (i = 0; i < arr_len; i++)printf("%s  ", arr_str[i]);printf("\n");qsort(arr_str, arr_len, STR_SIZE, cmp_str_size);for (i = 0; i < arr_len; i++)printf("%s  ", arr_str[i]);printf("\n\n");printf("对字符串型数组按长度排序-(是不稳定的排序算法，因此在长度相等的情况下，结果分析比较复杂)\n");for (i = 0; i < arr_len; i++)printf("%s  ", arr_str[i]);printf("\n");qsort(arr_str, arr_len, STR_SIZE, cmp_str_len);for (i = 0; i < arr_len; i++)printf("%s  ", arr_str[i]);printf("\n\n");printf("对结构体按照变量排序\n");stu arr_class[3] = { {17,185.5,190.8}, {16,160.9,200.7}, {18,120.3,150.5} };arr_len = sizeof(arr_class) / sizeof(arr_class[0]);for (i = 0; i < 3; i++){printf("%.1f  ", arr_class[i].weight);}printf("\n");qsort(arr_class, arr_len, sizeof(arr_class[0]), cmp_by_weight);for (i = 0; i < 3; i++){printf("%.1f  ", arr_class[i].weight);}printf("\n\n");return 0;
}

运行结果：