深圳住房建设局网站申报发布新闻稿
1.随机变量X
1.通常认知的"x"与随机变量X
我们通常意义上的 x 是自变量,y = f(x) 中的自变量。
但是 X 更多意义是 对应法则 " f " ,X完整写法是 X(ω) ω ∈ Ω。
X这个对应法则,可以将样本点映射到实数轴上。
那么X这个对应法则到底是什么,又怎么映射的呢?
2.两个实例解释 X 如何个映射法。
实例1:投一枚硬币,出现正面和反面的概率近似1/2.
实例2:明天下雨或者晴天的可能均为1/2.
现在我们定义为(实质上反应到数学表达上,即用X映射):

很明显,事件 “正 反 雨 晴”是样本点 ω ,这些事件反应到数轴上即为:“0 1” ,“ 1 0”.
而表格可知,这两个不同的场景都遵循一个规则:
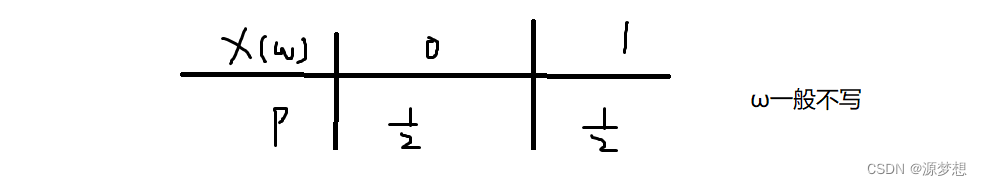
都抽象成了 X(ω) 这种规则,即 " X(ω) "将现实中的事件,变成了抽象的数字,方便进行数学处理,如:我们可以引入 微积分 这种强大的工具。
也可以说:随机变量 X 将一个随机不确定的过程,带入了又具体表示的数学世界,将“凌乱的概率” 变的有迹可循(如:我们可以用F(x) 表示X的概率分布)。
3.回过头看随机变量 X 的定义
设随机试验 E 的样本空间 Ω = { ω } ,如果对于每一个 事件ω ∈ Ω,都有唯一的实数 x ∈ R 与之对应。并且 对于 ∀x ∈ R ,有 {ω | X <= x, ω ∈ Ω}是随机事件,则称定义在 Ω 上的实值单值函数 X(ω) 为随机变量,记 X.
定义的意思是:随机变量是:“定义在样本空间 Ω 上,而取决于实数轴的函数”叫随机变量。
2.X 的分布函数 F(X) 的理解。
1.定义
设 X 是一个随机变量,称函数 F(x) = p { X<= x } (x ∈ R), 为随机变量 X 的分布函数,或称 X 服从F(X) 分布,记 X ~ F(x)。
2.解析定义
①X 的分布函数
分布,即概率。“X的分布函数",又可以说 “X的概率函数”。
通常有:幂函数,指数函数,三角函数。我们发现“幂 指数 三角”都反应了这种函数的规则 “f” (f也可以看作一个过程)。类比,”X的概率函数“是否反应了某种规则呢?
当然,“X的概率函数”也反应了一种规则。即 概率 。之所以我们很难理解 F(x) 是因为它的对应法则不符合我们通常的认知。
什么什么?概率也能是规则?当然可以对应法则(映射)是一个过程,那么 求 概率为何不能是一个过程呢?
重点:综上,那么 ”X的分布函数 F(x) = p{X<=x} " 即将 “{X<=x}” 这一坨东西,经过“P”求概率的过程,最终映射成了F(x), 故F(x)就是概率.
那么我们接下来的疑问就是, “{X <= x}”这一坨了,它是个啥?凭啥它就可以求概率了?
它还真可以求,因为"{X <= x}"表示的是一个或多个 “样本点” 或 “事件” 。事件当然可以求概率,为啥它就表示样本点了呢?
重点:由上对 X 的理解,X是将样本点映射到 数轴 上的一种法则,记X(ω) ,ω ∈ Ω
则 X 与 “x” (数轴上的点) 关系为 x = X(ω)。现在我们给出 x 的范围,即 " {X <= x} "是不是反解的结果就是样本点 ω 。
至此,我们已经完整知晓了 “x” 是怎样求出概率的,是通过 随机变量 X ,反解出 ω ,再通过 p 这个过程求出的 概率 F(x)。
而分布函数 F(x) 的对应法则 “F” 正是反应了这一过程,也因此,由于”X“ 规则的不同,导致 F(x) 规则的不同 常见有:

②F(x) = p { X<= x }
F(x) = p { X<= x },求的是概率,由 x 经过两次映射,一次是 逆映射 通过X法则 反解出 样本点ω ,再通过一次正映射 p{ } 求出事件概率,两次映射规则,共同构成从实数轴x 到 现实具体事件概率 的 "F"法则。
注:这里并不关心 P{ } 如何映射的 以及 X 的规则又是个啥,我们只关心 F(x) 到底是个啥,到底干了啥,咋来的,为什么要来就可以了。
③ (x ∈ R)
因为 x 是数轴上的取值,当然是R(由上可知)
3.为啥F(x) 不叫 x 的分布函数,叫 X 的分布函数
①可能分布二字对于 事件来说 更合适些,x还没有经过 X 转换成 ω 。
②可能这样说不够形象,明确。
3.F(X) 的充要条件
1.F(x)的充要条件 <=> ①②③
①F(x)是不减函数
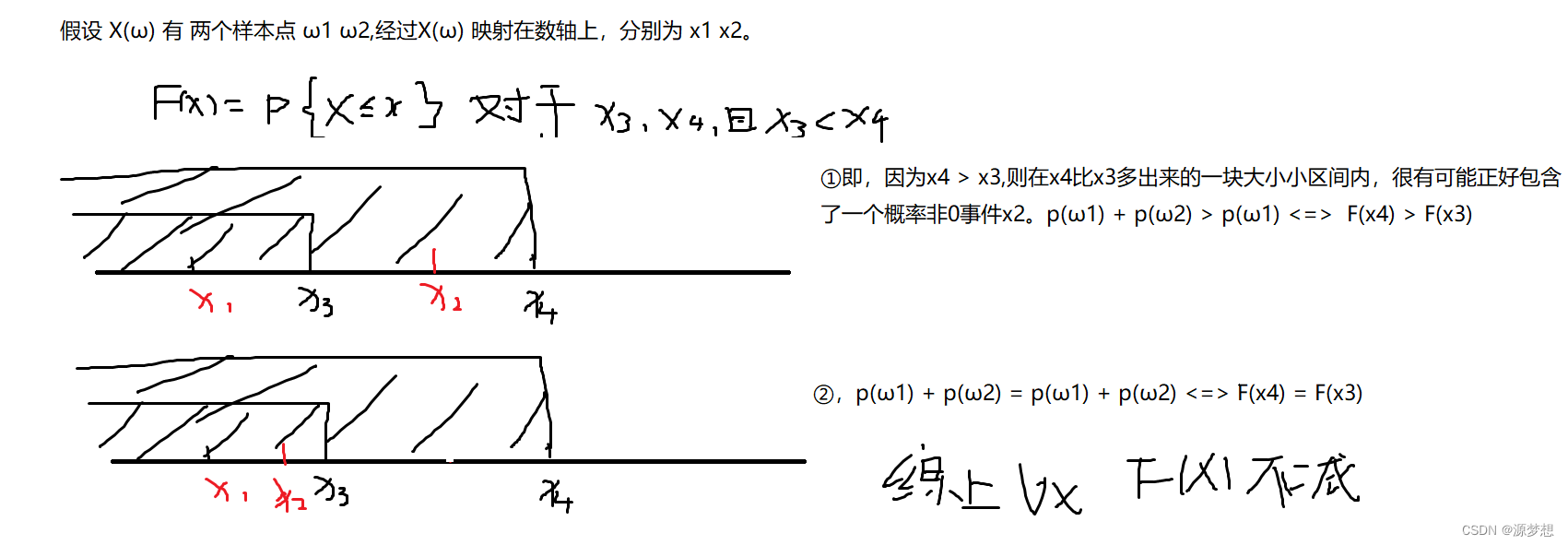
②F(x)是x0的右连续函数,x0 ∈ R。

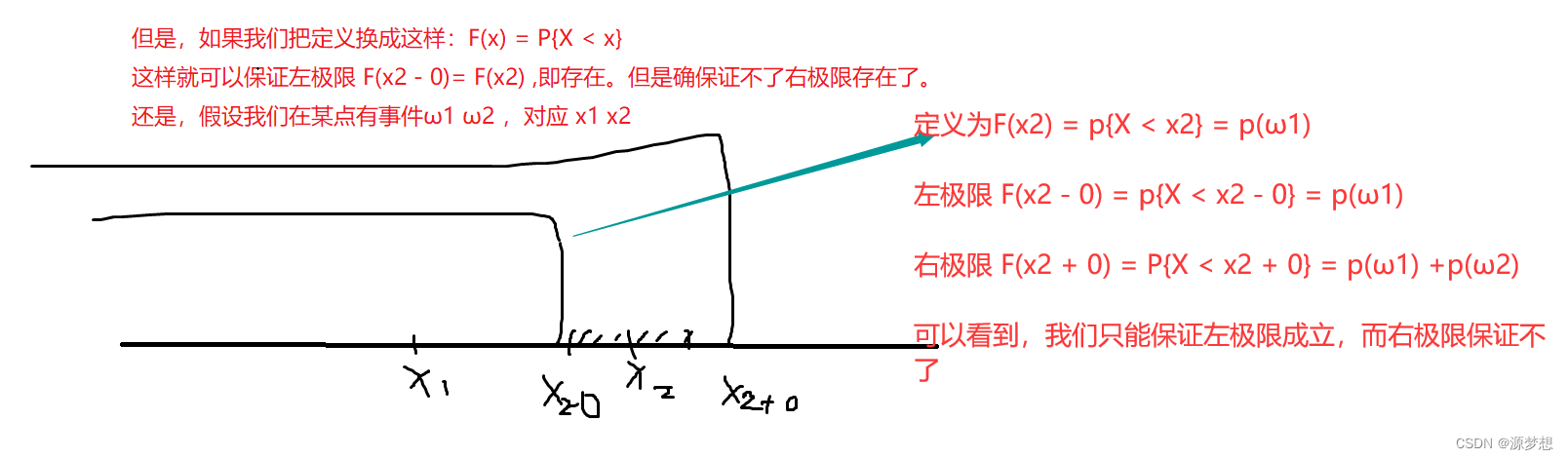
注:考研大纲明确规定,要求分布函数F(x)定义是F(x) = p{X <= x}
③F(-∞) = 0,F(+∞) = 1
F(-∞) = 0 , 一个事件不包含
F(+∞) = 1,包含全部事件。
4.经典例题
明天写
