榆林市行政效能建设网站谷歌浏览器 安卓下载2023版
特殊类型系统的最小拍无差设计
一般系统的最小拍无差设计
最小拍控制器的工程化改进
Dahlin算法
文章目录
- 特殊类型系统的最小拍无差设计
- 理论分析
- 典型输入函数的最小拍无差系统
- 一般系统的最小拍无差设计
- 有波纹最小拍无差设计
- 无波纹最小拍无差设计
- 最小拍控制器的工程化改进
- 针对输入信号类型敏感问题
- 针对模型参数变化敏感问题
- Dahlin算法
- 使用Dahlin算法设计控制器
- 振铃及其消除
直接设计和模拟设计法相对,是指直接基于计算机控制系统进行设计。
典型的计算机控制系统如图:
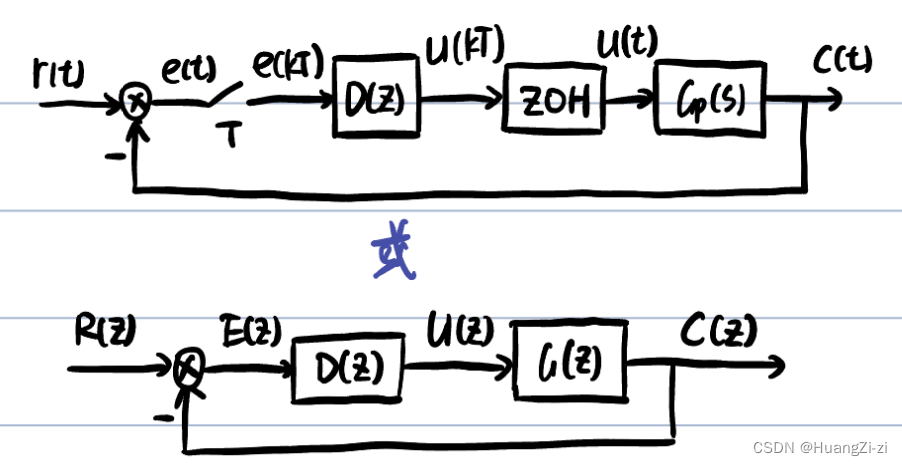
直接设计法的步骤:
- 根据控制系统性能指标或者其他约束条件,确定所需的闭环脉冲传函 ϕ ( z ) \phi(z) ϕ(z)
- 确定数字控制器的脉冲传函:

- 编写控制算法程序
特殊类型系统的最小拍无差设计
- 特殊类型系统:
(1)广义被控对象的脉冲传函 G ( z ) G(z) G(z)稳定
(2) G ( z ) G(z) G(z)中不含纯延时环节 - 最小拍无差:
在最少的几个采样周期内达到在采样时刻的输入和输出无误差。
理论分析
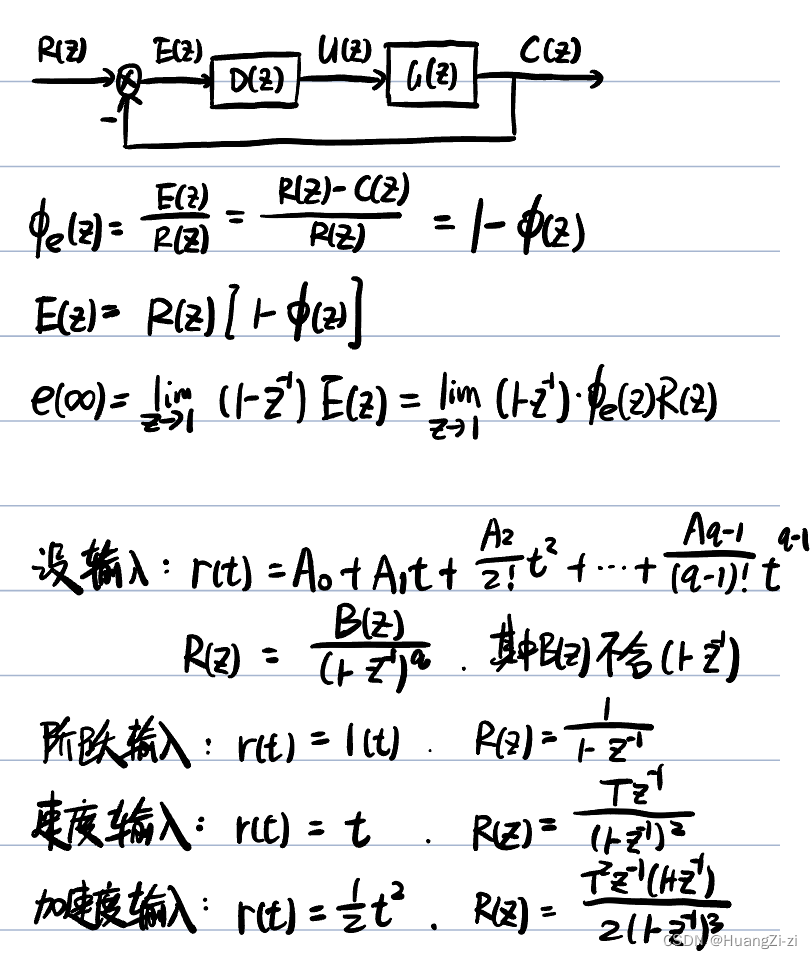

典型输入函数的最小拍无差系统
-
阶跃输入:
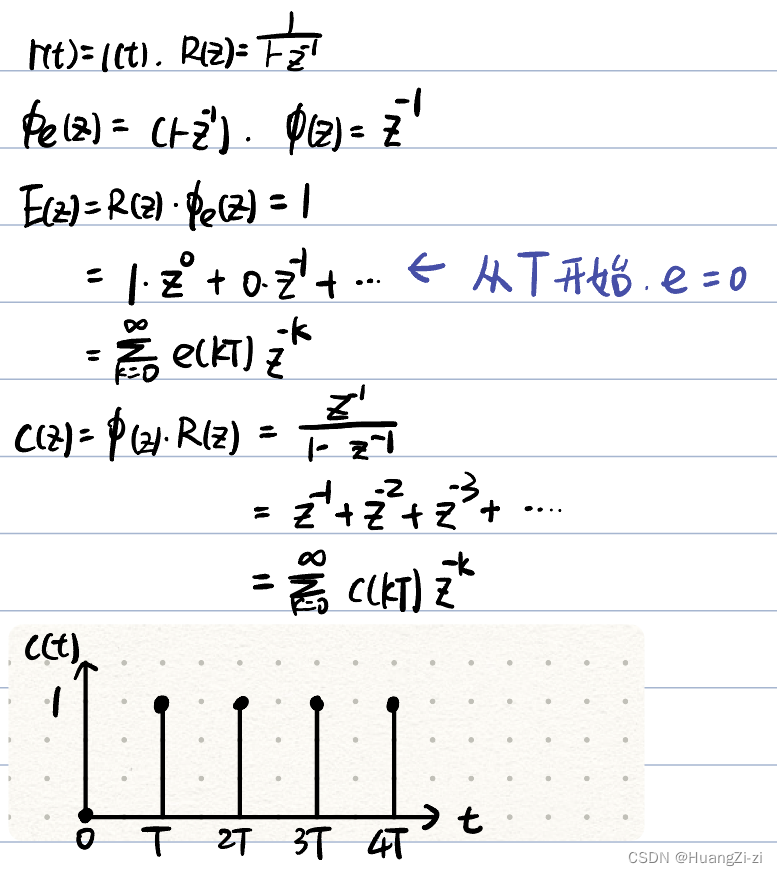
调节时间为T -
速度输入:
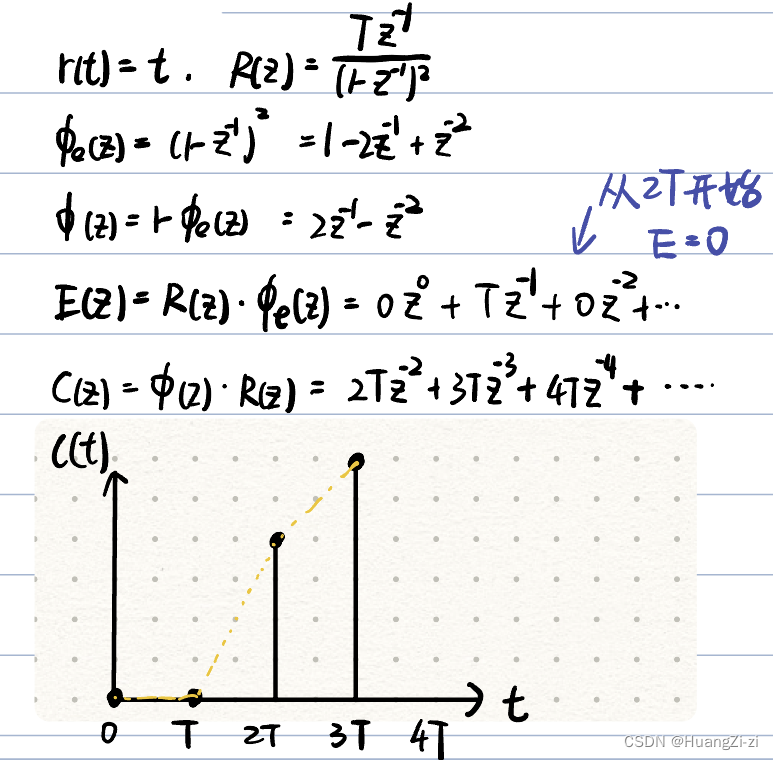
调节时间为2T -
加速度输入:
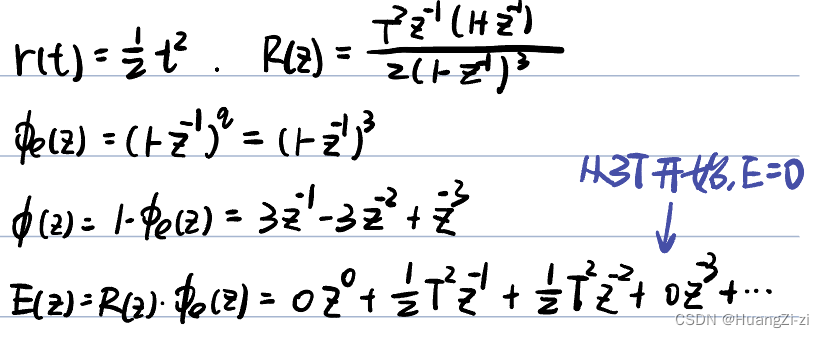
调节时间为3T
确定了 ϕ ( z ) \phi(z) ϕ(z)和 ϕ e ( z ) \phi_e(z) ϕe(z)以后,代入: D ( z ) = 1 G ( z ) ϕ ( z ) ϕ e ( z ) D(z)=\frac{1}{G(z)}\frac{\phi(z)}{\phi_e(z)} D(z)=G(z)1ϕe(z)ϕ(z)即可求出控制器的脉冲传函。
注意:针对一种典型输入函数设计的最小拍闭环脉冲传函 ϕ ( z ) \phi(z) ϕ(z)只适应这一种典型输入,不能适应各种输入。
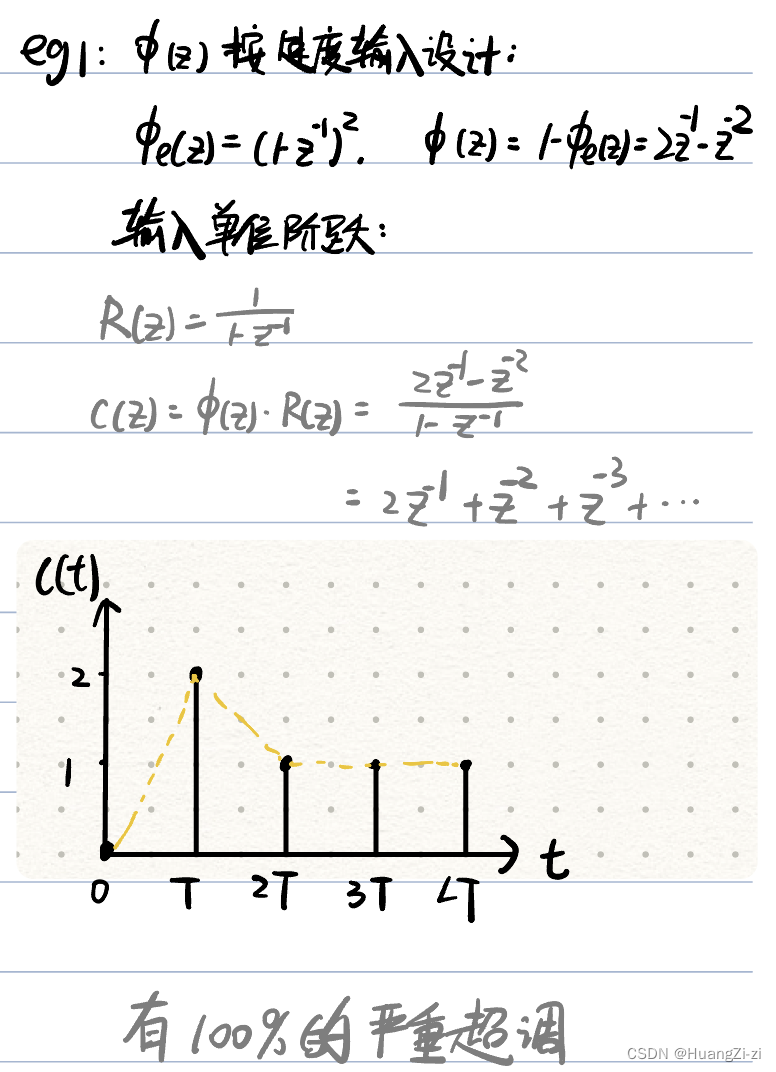
当输入次数较低的输入函数,会出现较大的超调、响应时间也增大,稳态误差为0
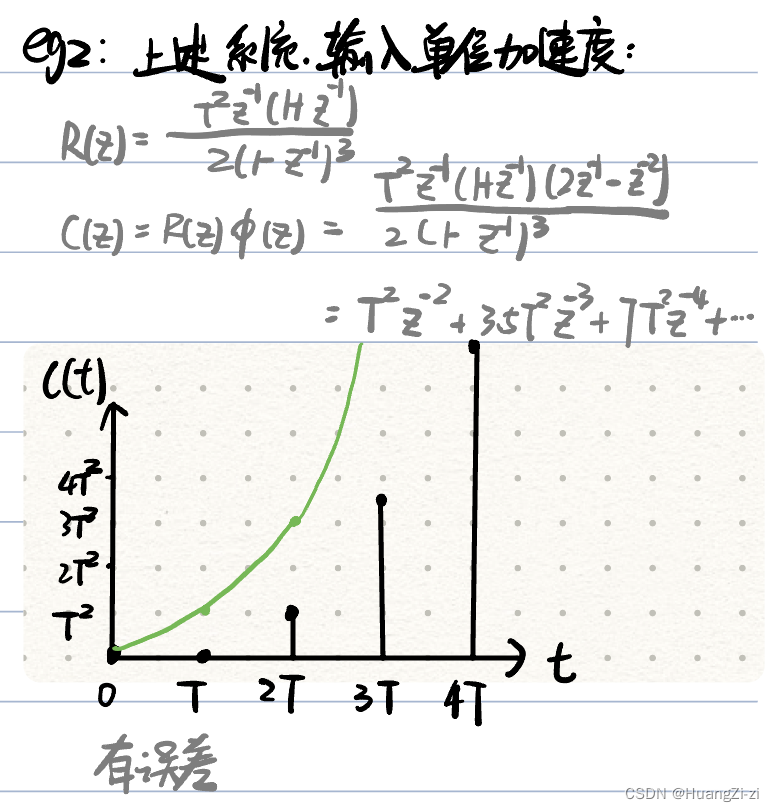
当输入次数较高的输入函数,输出不能完全跟踪输入,产生稳态误差
一般系统的最小拍无差设计
确定 ϕ ( z ) \phi(z) ϕ(z)的原则:



有波纹最小拍无差设计
也就是最一般的做法。遇到设计题没有特殊要求就这样做。


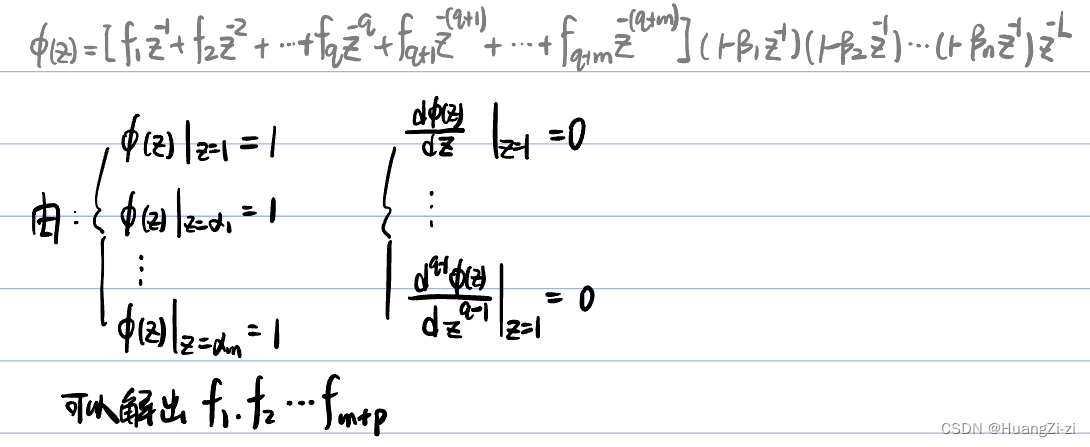
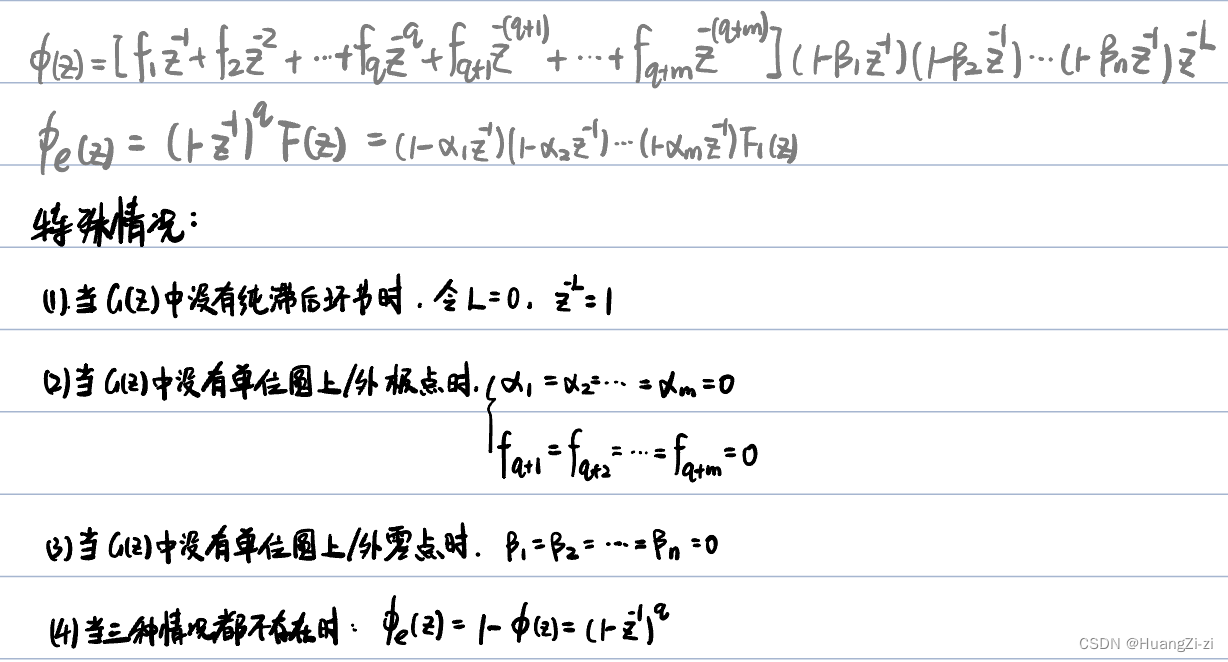
例题1:

例题2:

从这两道题可以看出:输出值可以跟随输入值。但控制器输出 u ( k ) u(k) u(k)不为常值,是震荡收敛的,因此在非采样时刻输出有误差,即有纹波(波纹)存在。
这样会浪费执行机构功率,增加机械磨损。
无波纹最小拍无差设计
需满足的条件:
- G ( z ) G(z) G(z)中有 q − 1 q-1 q−1个积分环节,q为输入型别
- 满足稳定性、物理可实现性
- ϕ ( z ) \phi(z) ϕ(z)中应包含 G ( z ) G(z) G(z)的所有零点
设计方法:

与有波纹的设计相比,区别在于:这次 ϕ ( z ) \phi(z) ϕ(z)包含了 G ( z ) G(z) G(z)的所有零点
例题3:


对比例题2和例题3,可以看出,无波纹设计,跟踪时间更长。
最小拍控制器的工程化改进
针对输入信号类型敏感问题
使用阻尼因子法。即在闭环脉冲传函中引入附加的阻尼因子,使输出偏差不立即为0,而是呈现一定的阻尼衰减特性,逐渐为0.
缺点是过渡时间增加
优点是输出对于不同信号的适应性有所改善

例题:


针对模型参数变化敏感问题
使用非最小的有限拍系统
把系统闭环脉冲传函的幂次提高1到2阶,使输出比最小拍多1到2拍才到达稳态。此时有更多可以设计的系数,即有更大的设计自由度,降低了模型参数变化的影响。


Dahlin算法
当要求系统没有超调或者超调很小时,不适用最小拍控制器。且实际工程中有很多纯滞后较大的系统,此时我们更加注意超调小或无超调,而允许调节时间为多个采样周期。
针对具有大滞后的一阶和二阶惯性环节,可以使用大林算法(Dahlin算法)
基本思路为:设计控制器,使得整个系统的闭环传函为带纯滞后的一阶环节。且闭环的纯滞后时间等于被控对象的纯滞后。
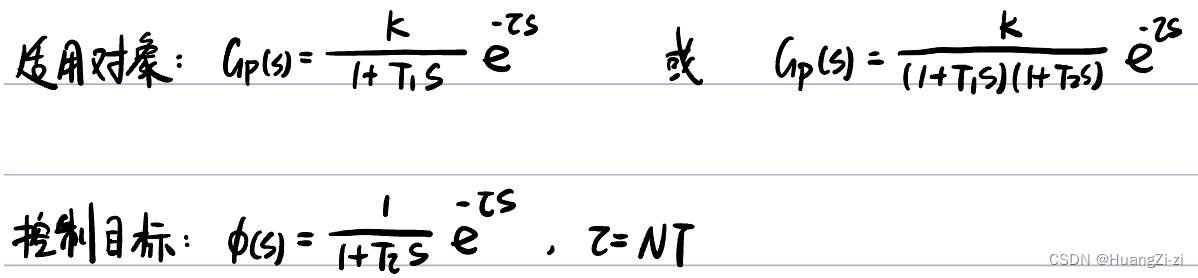
使用Dahlin算法设计控制器

根据被控对象是一阶还是二阶,方法比较固定,套公式就行:

例题1:

例题2:

振铃及其消除
在上面的例题2中可以看到,控制器的输出有大幅度的衰减震荡(意思是震荡幅度大,但振幅衰减),频率为1/2采样频率。这种现象叫做振铃。
- 振铃与波纹
- 振铃:由于被控对象中惯性环节的低通特性引起,对于输出没有影响,但增加了执行机构的磨损。
- 波纹:由于控制器输出震荡,引起输出一直有波动
-
振铃现象分析


T → 0 T\to0 T→0, z 2 = − C 2 C 1 → − 1 z_2=-\frac{C_2}{C_1}\to-1 z2=−C1C2→−1,易产生振铃,因此 T T T可以适当增大 -
振铃幅度RA

-
振铃的消除


-
工程中关键参数的选择
- 根据需要确定 T τ T_\tau Tτ和 R A RA RA的指标
- R A = C 2 C 1 − e − T T τ + e − T T 1 + e − T T 2 RA=\frac{C_2}{C_1}-e^{-\frac{T}{T_\tau}}+e^{-\frac{T}{T_1}}+e^{-\frac{T}{T_2}} RA=C1C2−e−TτT+e−T1T+e−T2T。通过上式计算T
- N = τ / T N=\tau /T N=τ/T,确定N
- 计算 G ( z ) G(z) G(z)和 ϕ ( z ) \phi(z) ϕ(z)
- 求 D ( z ) D(z) D(z)
