企业服务公司起名抖音优化是什么意思
前言
二叉搜索树(BST)存在一个问题:当你添加的节点数够多的时候,树的一边可能会非常的深。而其他的分支却只有几层。

AVL树
为了解决上面的问题,我们提出一种自平衡二叉搜索树。意思是任何一个节点左右两侧子树的高度之差最多为1。
添加或移除节点时,AVL树会尝试自动保持自平衡,任意一个节点(无论深度)的左右子树高度最多相差1。添加或移除节点时。AVL树会尽可能尝试转换为完全数。
节点的高度
节点的高度是从节点到其任意子节点的边的最大值。

那么我们怎么计算某个节点的高度呢?
因为我们并无法事先知道树的哪一层里的左分支深还是右分支深。所以我们需要进行层层比较,层层返回其左右分支深度的最大值。
getNodeHeight(node) {if (node == null) {return -1;}return Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1;
}递归:
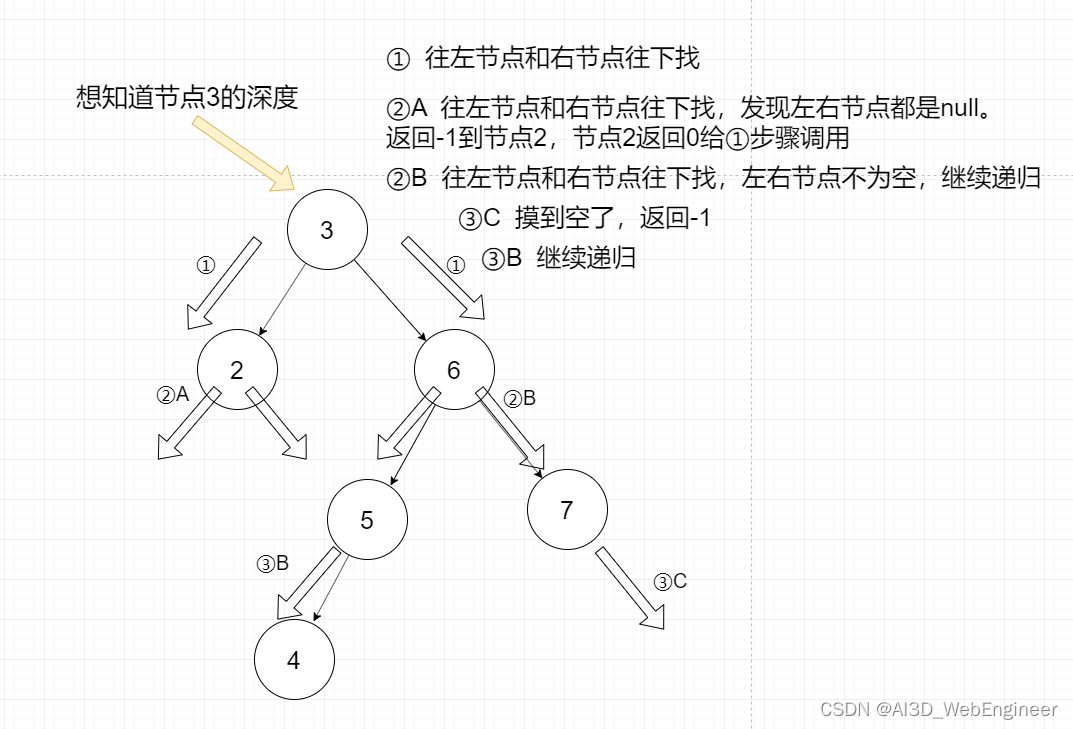
递归后的调用:
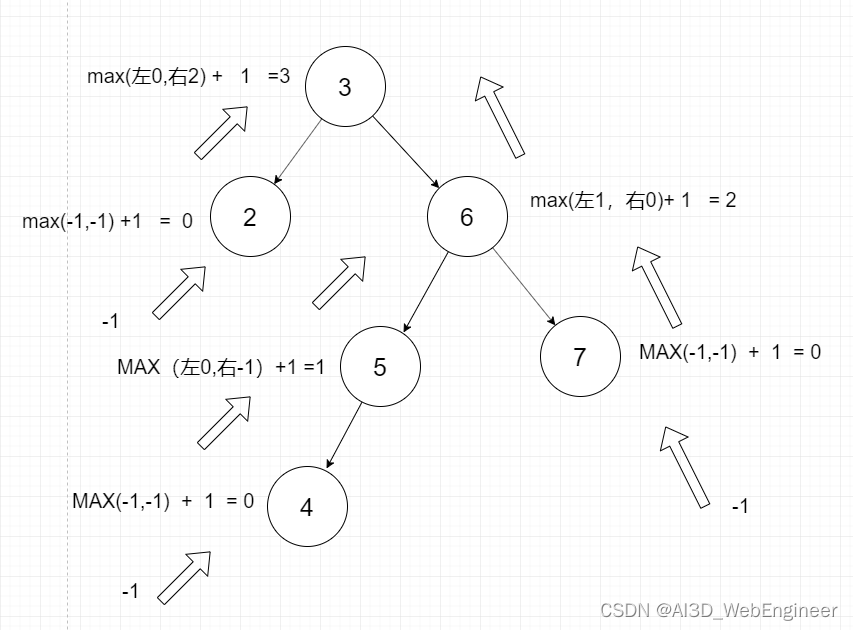
平衡因子
一段能平衡树节点的逻辑。在AVL数中,需要对每个节点计算左子树高度(hl)和右子树高度(hr)。并取其差值。如果差值hr - hl或者hl-hr不为0(一样深),1或-1(只差1个深度)。则需要平衡该AVL树。这就是平衡因子的概念。
我们一般以hr-hl作为平衡因子。

可以看到,我们刚才的例子,并不是一颗平衡树。因为节点3的平衡因子为2。也就是节点3的左子树和右子树不平衡。
计算某个节点的左右子树高度差应该很简单了
getBalanceFactor(node) {const heightDifference = this.getNodeHeight(node.left) - this.getNodeHeight(node.right);
}当高度差大于1的时候,我们就需要对数进行自平衡了。
树的旋转
叉树中任意节点的左右子树的高度差都不大于1。当插入或删除一个节点时,我们需要通过一次或多次树的「旋转」来保持二叉树的平衡。
树的旋转分为「左旋」和「右旋」两种具体操作,这两种操作是完全相反的,互为逆操作。
左旋是「将该节点的右子树逆时针旋转」,右旋是「将该节点的左子树顺时针旋转」。
对于一个节点node进行左旋操作时,具体操作为:「将node.right子树取下,node.right节点称为新的根节点newRoot,将node接在newRoot的左节点,newRoot.left取下接在node的右节点上。」
右旋操作相反:「将node.left子树取下,node.left节点作为新的根节点newRoot,将node接在newRoot的右节点,newRoot.right取下接在node的左节点上。」
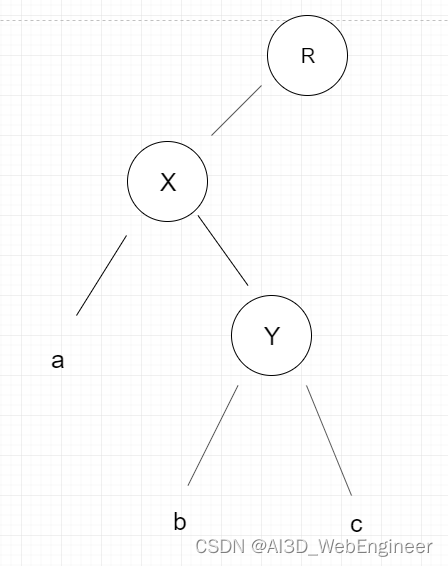
先看这个树,已知的大小关系存在:R>c > Y> b >X >a

右旋RR:【子节点左边多右边少,向右单旋转】 适用于左侧子节点的高度大于右侧子节点的高度,且左侧子节点也是平衡或左侧较重。
左旋LL:【子节点右边多左边少,向左单旋转。适用于左侧节点高度小于右侧子节点高度,且右侧子节点也是平衡或右侧较重
看到这里你可能会觉得疑惑,什么叫平衡或较重?不急,后面自然会解释。

简而言之左旋就是把右树节点放自己头上。右旋就是把左树节点放自己头上
左旋后右旋,便回到最原本的树结构。

左旋代码:RR
rotationRR(node) {// node对应的是X X包含了左右树节点,修改后返回出去// 拿出右节点Yconst tmp = node.right;// 把Y的左节点b拿出来放到X,即node的右节点node.right = tmp.left;// 把X放到Y的左树tmp.left = node;// 返回Yreturn tmp;}右旋代码:LL
rotationLL(node) {const tmp = node.left;node.left = tmp.right;tmp.right = node;return tmp;}这样就结束了吗?当然不是。上面的旋转只是向左向右的单旋转。
AVL不平衡存在四种情况:
第一种情况:R节点的左侧子节点高度高于右侧节点。且R节点的左侧子节点a的子节点(Y-b)重于a的右侧子节点(无)。此时就可以使用我们上面的右旋做法。
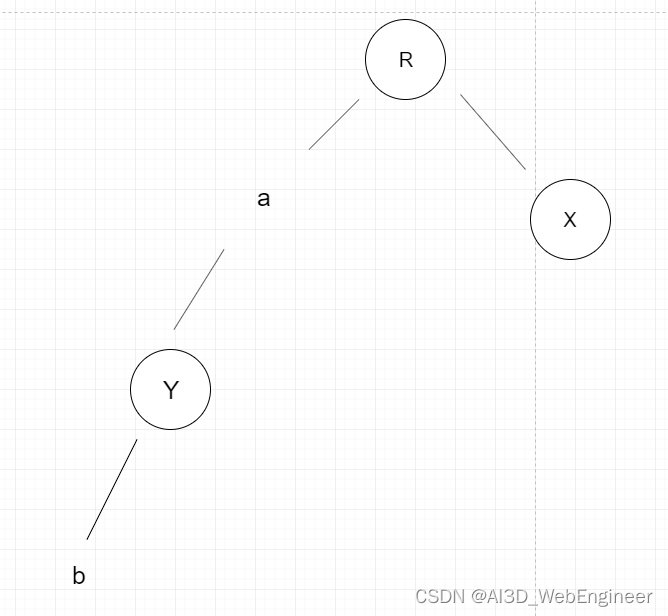
右旋得到:

第二种情况:R节点的右侧子节点高度高于左侧节点。且R节点的右侧子节点a的子节点(Y-b)重于a的左侧子节点(无)。此时就可以使用我们上面的左旋做法。

左旋得到:

第三种情况:R节点的左侧子节点高度高于右侧节点。且R节点的左侧子节点a的子节点(Y-b)重于a的右侧子节点(无)。

如果此时直接右旋:

依然不平衡。所以这种情况我们需要做两次旋转。

代码:
rotationLR(node) {node.left = this.rotationRR(node.left);return this.rotationLL(node);
}第四种情况:右侧子节点的高度高于左侧子节点,并且右侧子节点左侧较重。这种情况下我们可以对右侧子节点进行有旋转来修复。然后再对不平衡节点进行一个左旋转来修复。

向AVL树中插入节点
前面讲解了这么多树的旋转,就是为了服务于AVL树中节点的增删。
步骤很简单,每当我们向AVL树里插入或删除一个节点,便执行平衡性检查。平衡性不通过,便旋转树。
const BalanceFactor = {UNBALANCED_RIGHT: 1,SLIGHTLY_UNBALANCED_RIGHT: 2,BALANCED: 3,SLIGHTLY_UNBALANCED_LEFT: 4,UNBALANCED_LEFT: 5
};
getBalanceFactor(node) {const heightDifference = this.getNodeHeight(node.left) - this.getNodeHeight(node.right);switch (heightDifference) {case -2:return BalanceFactor.UNBALANCED_RIGHT;case -1:return BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT;case 1:return BalanceFactor.SLIGHTLY_UNBALANCED_LEFT;case 2:return BalanceFactor.UNBALANCED_LEFT;default:return BalanceFactor.BALANCED;}
}·左子树高度-右子树高度。当差值为0(default)或-1或1,都属于平衡范围。而2和-2则已经不平衡。-1和1方便让我们辨别哪侧子树较重。
insert(key) {this.root = this.insertNode(this.root, key);}insertNode(node, key) {if (node == null) {return new Node(key);} else if (this.compareFn(key, node.key) === Compare.LESS_THAN) {node.left = this.insertNode(node.left, key);} else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {node.right = this.insertNode(node.right, key);} else {return node; // duplicated key}// verify if tree is balancedconst balanceFactor = this.getBalanceFactor(node);if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {if (this.compareFn(key, node.left.key) === Compare.LESS_THAN) {// Left left casenode = this.rotationLL(node);} else {// Left right casereturn this.rotationLR(node);}}if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {if (this.compareFn(key, node.right.key) === Compare.BIGGER_THAN) {// Right right casenode = this.rotationRR(node);} else {// Right left casereturn this.rotationRL(node);}}return node;}从AVL树里移除节点
removeNode(node, key) {node = super.removeNode(node, key); // {1}if (node == null) {return node;}// verify if tree is balancedconst balanceFactor = this.getBalanceFactor(node);if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {// Left left caseif (this.getBalanceFactor(node.left) === BalanceFactor.BALANCED ||this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) {return this.rotationLL(node);}// Left right caseif (this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) {return this.rotationLR(node.left);}}if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {// Right right caseif (this.getBalanceFactor(node.right) === BalanceFactor.BALANCED ||this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) {return this.rotationRR(node);}// Right left caseif (this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) {return this.rotationRL(node.right);}}return node;}